Arabski sposób rozwiązywania równań kwadratowych

Perski matematyk Alchwarizmi w dziele Hisab al-dżabr wa-al mukabala czyli Sztuka redukcji i przenoszenia zawarł swoje rozważania na temat rozwiązań równań liniowych i kwadratowych. Praca zawiera kompletne rozwiązania równań stopnia pierwszego i drugiego. Ponieważ nie uznawano wówczas liczb ujemnych, równań kwadratowych były trzy rodzaje.
x² + ax = b, x² + b = ax, x² = ax + b,

A oto arabski sposób rozwiązywania równań kwadratowych x² + ax = b

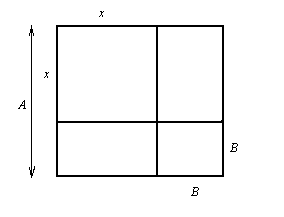
równanie kwadratowe
Kreślimy kwadrat o boku długości A, wycinamy w rogu kwadrat o boku x. W przeciwległym rogu kwadrat o największym możliwym boku B. Kwadrat dopełniają dwa prostokąty o bokach x i B. Mamy równanie A² = x² + B² + 2Bx. Znamy wartości a i b, poszukujemy A i B.

$B = \frac{a}{2}$ , $B^{2} = \frac{a^{2}}{4}$ , $A^{2} = b + B^{2} = b + \frac{a^{2}}{4}$ ,

Ostatecznie $x = A - B = \sqrt{A^{2}} - B = \sqrt{b + \frac{a^{2}}{4}} - \frac{a}{2}$ ,

Rozważmy przykład x² + 12x = 45

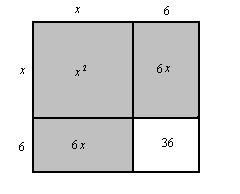Wykreślmy kwadrat o boku x, dorysujmy prostokąty, których jeden z boków jest równy połowie współczynnika przy x, czyli 6. Zacieniowaną figurę na rysunku, utworzoną z kwadratu i dwóch prostokątów, greccy matematycy nazywali gnomonem. Nasz gnomon x² + 12x ma pole równe 45. Dopełniamy nasz gnomon do pełnego kwadratu, którego bok ma długość x + 6. Pole całego kwadratu równe jest 45 + 36 = 81. Otrzymujemy równanie (x + 6)² = 81, skąd x + 6 = 9. Zostało oczywiście pominięte nieznane wtenczas rozwiązanie ujemne, ostatecznie otrzymujemy x = 3.

Zastosujmy tą metodę dla równania kwadratowego innego typu niż podane powyżej, na przykład x² + 8x + 7 = 0

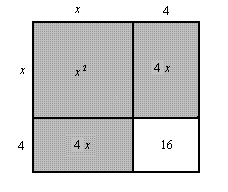
Po przekształceniu otrzymujemy x² + 8x = -7. Pole gnomonu musi więc równać się -7! Pomimo tej niedorzeczności liczmy dalej sposobem arabskim. Bok małego kwadratu równy jest 4, więc pole jego wynosi 16. Cały kwadrat ma więc pole -7 + 16 = 9. Mamy więc (x + 4)² = 9, stąd x + 4 = 3 lub x + 4 = -3, Otrzymujemy dwa rozwiązania x = -1 lub x = -7, które są poprawne, pomimo iż po drodze spotkaliśmy niedorzeczność. Ten sposób zawsze działa, można więc rozwiązywać równania kwadratowe bez odwoływania się popularnej delty.