Geometria, zadanie nr 1618
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
kkam post贸w: 1 |  2012-03-27 17:10:47Zadanie 1/ Dla jakich warto艣ci parametru m prosta 2x-y+m-1=0 jest styczna do okr臋gu x2+y2=6 Zadanie 2/ okr膮g o r贸wnaniu x2-6x+y2-2y+2=0 i prosta x+2y+2=0 przecinaj膮 si臋 w punktach A,B. Wyznacz wsp贸艂rz臋dne tych punkt贸w. Dzi臋kuje za Pomoc! zadanie 1 wyznacz r贸wnianie okr臋gu opisanego na kwadracie abcd je艣li przeciwleg艂e wierzcho艂ki a i c tego kwadratu maj膮 wsp贸艂rz臋dne A(-3,-2), C(2,1) zadanie 2 Podaj r贸wnania stycznych do okr臋gu (x-2)2+(y-1)2=16 r贸wnoleg艂ych do osi 0y zadanie 3 okre艣l wzajemne po艂o偶enie okr臋g贸w (x-2)2+(y+3)2=49 i x2+y2=9 x2+y2+2x=0 i x2+y2+12x+24y+36=0 |
marcin2002 post贸w: 484 | 2012-03-27 17:20:47 wyznacz r贸wnianie okr臋gu opisanego na kwadracie abcd je艣li przeciwleg艂e wierzcho艂ki a i c tego kwadratu maj膮 wsp贸艂rz臋dne A(-3,-2), C(2,1) 艢rodek odcinka AC jest 艣rodkiem okr臋gu a odcinek AC 艣rednic膮 okr臋gu $|AC|=\sqrt{[2-(-3)]^2+[1-(-2)]^2}$ $|AC|=\sqrt{5^2+3^2}$ $|AC|=\sqrt{25+9}$ $|AC|=\sqrt{34}$ $r=\frac{\sqrt{34}}{2}$ $ S_{AC}=(\frac{-3+2}{2};\frac{-2+1}{2})$ $S_{AC}=(\frac{-1}{2};\frac{-1}{2})$ R脫WNANIE OKR臉GU $(x+\frac{1}{2})^2+(y+\frac{1}{2})^2=(\frac{\sqrt{34}}{2})^2$ $(x+\frac{1}{2})^2+(y+\frac{1}{2})^2=\frac{34}{4}$ |
marcin2002 post贸w: 484 | 2012-03-27 17:27:36 OKRE艢L WZAJEMNE PO艁O呕ENIE OKR臉G脫W pierwszy okr膮g $(x-2)^2+(y+3)^2=49 $ drugi okr膮g $ x^2+y^2=9 $ dla pierwszego $S_{1}=(2,-3)$ $r=7$ dla drugiego $S_{2}=(0,0)$ $R=3$ LICZYMY D艁UGO艢膯 ODCINKA $S_{1}S_{2}$ $|S_{1}S_{2}|=\sqrt{2^{2}+(-3)^2}$ $|S_{1}S_{2}|=\sqrt{13}$ $|S_{1}S_{2}|\approx3,61$ $r+R=7+3=10$ $|S_{1}S_{2}|<r+R$ drugi okr膮g le偶y wewn膮trz pierwszego |
marcin2002 post贸w: 484 | 2012-03-27 17:35:01 OKRE艢L WZAJEMNE PO艁O呕ENIE OKR臉G脫W pierwszy okr膮g $x^2+y^2+2x=0 $ drugi okr膮g $x^2+y^2+12x+24y+36=0 $ pierwszy okr膮g $(x+1)^2-1+y^2+=0 $ drugi okr膮g $(x+6)^2-36+(y+12)^2-144+36=0 $ pierwszy okr膮g $(x+1)^2+y^2+=1 $ drugi okr膮g $(x+6)^2+(y+12)^2=144 $ dla pierwszego $S_{1}=(-1,0)$ $r=1$ dla drugiego $S_{2}=(-6,-12)$ $R=12$ LICZYMY D艁UGO艢膯 ODCINKA $S_{1}S_{2}$ $|S_{1}S_{2}|=\sqrt{[-6-(-1)]^2+(-12)^2}$ $|S_{1}S_{2}|=\sqrt{(-5)^2+(-12)^2}$ $|S_{1}S_{2}|=\sqrt{25+144}$ $|S_{1}S_{2}|=\sqrt{169}$ $|S_{1}S_{2}|=13$ $r+R=1+12=13$ $|S_{1}S_{2}|=r+R$ okr臋gi s膮 zewn臋trznie styczne |
marcin2002 post贸w: 484 | 2012-03-27 17:38:07 Podaj r贸wnania stycznych do okr臋gu $(x-2)^2+(y-1)^2=16$ r贸wnoleg艂ych do osi 0y $r=4$ $S=(2;1)$ r贸wnania prostych $x=-2 $ i $ x=6$ |
marcin2002 post贸w: 484 | 2012-03-27 17:49:28 DO POSTU WY呕EJ  |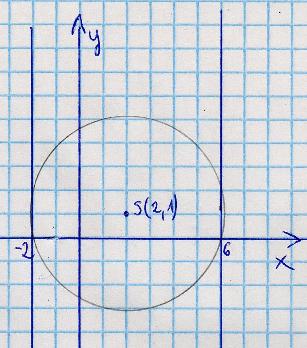
marcin2002 post贸w: 484 | 2012-03-27 17:49:46 Dla jakich warto艣ci parametru m prosta $2x-y+m-1=0$ jest styczna do okr臋gu $x^2+y^2=6$ Odleg艂o艣膰 艣rodka okr臋gu od prostej musi by膰 r贸wna promieniowi czyli $\sqrt{6}$ $\frac{|m-1|}{\sqrt{2^{2}+(-1)^{2}}}=\sqrt{6}$ $\frac{|m-1|}{\sqrt{4+1}}=\sqrt{6}$ $|m-1|=\sqrt{30}$ $m-1=\sqrt{30}$$\vee$$m-1=-\sqrt{30}$ $m=1+\sqrt{30}$$\vee$$m=1-\sqrt{30}$ |
agus post贸w: 2387 | 2012-03-27 18:21:27 2) Sprawd藕 r贸wnanie okr臋gu i r贸wnanie prostej, bo mi wysz艂o,偶e nie maj膮 punkt贸w wsp贸lnych. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj