Planimetria, zadanie nr 1636
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
witam24 post贸w: 14 |  2012-03-29 15:34:401.Jeden z k膮t贸w ostrych tr贸jk膮ta prostok膮tnego ma miar臋 $\alpha$. Oblicz stosunek wysoko艣膰i poprowadzonej z wierzcho艂ka k膮ta prostego do promienia okr臋gu wpisanego w ten tr贸jk膮t . 2. Na okr臋gu o promieniu 1 opisano tr贸j膮t prostok膮tny , kt贸rego przyprostok膮ne maj膮 d艂ugo艣膰i x i y a) Wyznacz y jako funkcj臋 x i okre艣l dziedzin臋 tej funkcji . 3. D艂ugo艣膰i bok贸w tr贸jk膮ta s膮 kolejnymi wyrazami ci膮u arytmetycznego . Obw贸d tr贸jk膮ta jest r贸wny 21 , a cosinus najwi臋kszego k膮ta $-$0,1 . Oblicz d艂ugo艣膰i bok贸w tego tr贸jk膮a . 4.D艂ugo艣膰i bok贸w tr贸jk膮ta prostok膮tnego tworz膮 rosn膮cy ci膮g arytmetyczny . Wyka偶 , 偶e jego r贸偶nica jest d艂ugo艣ci膮 promienia okr臋gu wpisaneg w ten tr贸jk膮t . 5.Kr贸tszy bok r贸wnoleg艂oboku ma d艂ugo艣膰 3 . Dwa okr臋gi o promieniu 1 wpisano w r贸wnoleg艂obok w taki spos贸b , 偶e oba okr臋gi s膮 stycznie zewn臋trznie i ka偶dy z nich jest styczny do trzech bok贸w r贸wnoleg艂oboku Oblicz d艂ugo艣c d艂u偶szego boku r贸wnoleg艂oboku . |
marcin2002 post贸w: 484 | 2012-03-29 16:36:24 ZADANIE 1 RYSUNEK  |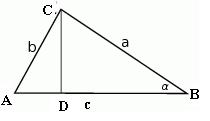
marcin2002 post贸w: 484 | 2012-03-29 16:36:50 ZADANIE 1 OBLICZENIA ZE WZOR脫W NA POLE TR脫JK膭TA WYZNACZAM PROMIE艃 I WYSOKO艢膯 $P=\frac{1}{2}r(a+b+c)\Rightarrow r=\frac{2P}{a+b+c}$ $\frac{1}{2}c\cdot h \Rightarrow h=\frac{2P}{c}$ $\frac{h}{r}=\frac{\frac{2P}{c}}{\frac{2P}{a+b+c}}=\frac{a+b+c}{c}=\frac{a}{c}+\frac{b}{c}+1=cos\alpha+sin\alpha+1$ |
marcin2002 post贸w: 484 | 2012-03-29 16:51:14 ZADANIE 3 RYSUNEK  |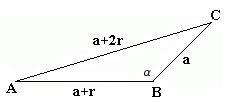
marcin2002 post贸w: 484 | 2012-03-29 16:51:40 ZADANIE 3 OBLICZENIA a ; a+r ; a+2r - d艂ugo艣ci bok贸w $a+a+r+a+2r=21 \Rightarrow 3a+3r=21 \Rightarrow r=7-a$ ZATEM D艁UGO艢CI BOK脫W TR脫JK膭TA MAJ膭 a ; 7 ; 14-a ZAPISUJEMY TWIERDZENIE COSINUS脫W $|AC|^2=|AB|^2+|BC|^2-2\cdot|AB|\cdot|BC|cos\alpha$ $(14-a)^2=a^2+7^2-14a\cdot(-0,1)$ $196-28a+a^2=a^2+49+1,4a$ $29,4a=147$ $a=5$ a=5 b=7 c=14-5=9 BOKI TR脫JK膭TA MAJ膭 D艁UGO艢CI 5,7,9 |
marcin2002 post贸w: 484 | 2012-03-29 17:10:27 ZADANIE 5 RYSUNEK  |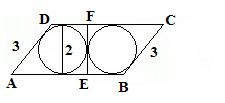
marcin2002 post贸w: 484 | 2012-03-29 17:10:57 ZADANIE 5 WYJA艢NIENIE R脫WNOLEG艁OBOK DZIELIMY NA DWA TRAPEZY PROSTOK膭TNE PROST膭 EF ZAUWA呕MY 呕E |AE|+|DF|=|AB| KA呕DY Z TYCH TRAPEZ脫W OPISANY JEST NA OKR臉GU Z WARUNKU OPISYWALNO艢CI CZWOROK膭TA NA OKR臉GU |AE|+|DF|=3+2 |AE|+|DF|=5 |AB|=5 D艁U呕SZY BOK R脫WNOLEG艁OBOKU JEST R脫WNY 5 |
agus post贸w: 2387 | 2012-03-29 17:15:34 2. promienie okr臋gu poprowadzone do punkt贸w styczno艣ci podziel膮 tr贸jk膮t prostok膮tny na 3 deltoidy, a przyprostok膮tna x na odcinki 1 i x-1, przyprostok膮tn膮 y na 1 i y-1, a przeciwprostok膮tn膮 na odcinki x-1 i y-1 (b臋dzie mie膰 d艂ugo艣膰 x+y-2) dla tr贸jk膮ta prostok膮tnego stosujemy tw. Pitagorasa $x^{2}+y^{2}=(x+y-2)^{2}$ $x^{2}+y^{2}=x^{2}+y^{2}+4+2xy-4x-4y$ 4y-2xy=4-4x /:2 2y-xy=2-2x y(2-x)=2-2x /:(2-x) y=$\frac{2-2x}{2-x}=\frac{2x-2}{x-2}=\frac{2x-4+2}{x-2}$= =$\frac{2x-4}{x-2}+\frac{2}{x-2}$=2+$\frac{2}{x-2}$ dziedzina funkcji: (2;+$\infty$) Wiadomo艣膰 by艂a modyfikowana 2012-03-29 17:44:56 przez agus |
agus post贸w: 2387 | 2012-03-29 17:43:58 4. x,x+r,x+2r boki tr贸jk膮ta prostok膮tnego, r>0 r贸偶nica ci膮gu arytmetycznego tw.Pitagorasa: $x^{2}+(x+r)^{2}=(x+2r)^{2}$ $x^{2}+x^{2}+2rx+r^{2}=x^{2}+4rx+4r^{2}$ $x^{2}-2rx-3r^{2}$=0 $\triangle$=16$r^{2}$ $\sqrt{\triangle}$=4r x=$\frac{2r+4r}{2}$=3r (drugi z pierwiastk贸w odrzucamy, bo jest ujemny) 3r,4r,5r- boki tr贸jk膮ta prostok膮tnego promienie (R) okr臋gu poprowadzone do punkt贸w styczno艣ci podziel膮 boki tr贸jk膮ta na odcinki (patrz zad.2) R i 3r-R, R i 4r-R, 3r-R i 4r-R zatem przeciwprostok膮tna ma d艂ugo艣膰 3r-R+4r-R=7r-2R czyli 7r-2R=5r 2r=2R r=R |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj