Stereometria, zadanie nr 1676

Autor	Zadanie / Rozwiązanie
aanuussiaa93 postów: 3	2012-04-03 20:02:46 W graniastosłupie prawidłowym czworokątnym przekątne sąsiednich ścian bocznych tworzą kąt alfa=30stopni. Wykonaj odpowiedni rysunek, zaznacz na nim kąt alfa oraz kąt beta, jaki tworzy przekątna ściany bocznej z krawędzią podstawy. Oblicz cos beta ( w obliczeniach przyjmij że sin alfa/2=(pierwiastek z 6 - pierwiastek z 2)/4

abcdefgh postów: 1255	2012-04-03 20:27:30 $\frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\frac{a\sqrt{2}}{2}}{d}$ $2\sqrt{2}a=d(\sqrt{6}-\sqrt{2})$ $\frac{2\sqrt{2}a(\sqrt{6}+\sqrt{2})}{\sqrt{6}-\sqrt{2}(\sqrt{6}+\sqrt{2})}$=d $\frac{4\sqrt{3}a-4a}{4}=d$ $d=(\sqrt{3}-1)a$ $cos\beta=\frac{a}{(\sqrt{3}-1)a}$ $cos\beta=\frac{\sqrt{3}+1}{(\sqrt{3}-1)*(\sqrt{3}+1)}$ $cos\beta=\frac{\sqrt{3}+1}{2}\approx 0,3660$ $\beta\approx69^o$

marcin2002 postów: 484	2012-04-03 20:55:36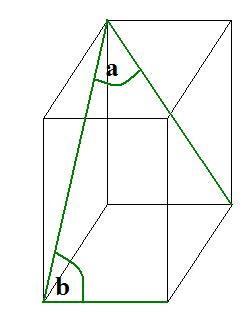

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj