Planimetria, zadanie nr 1800
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
fiukowa post贸w: 41 |  2012-05-02 11:14:30W prostok膮t wpisano trzy parami styczne okr臋gi w ten spos贸b, 偶e dwa z nich s膮 styczne do trzech bok贸w, prostok膮ta, a trzeci jest styczny do jednego z bok贸w prostok膮ta . Oblicz promie艅 mniejszego okr臋gu je偶eli promie艅 wi臋kszego okr臋gu jest r贸wny R . |
aididas post贸w: 279 | 2012-05-02 13:33:48 Ta sytuacja wygl膮da tak: 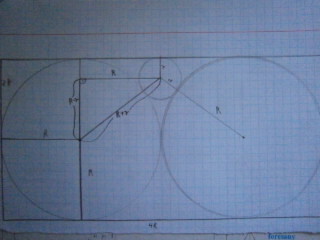 Jak wida膰 powstaje tam tr贸jk膮t prostok膮tny o danych bokach, wi臋c twierdzenie Pitagorasa wygl膮da tak: $R^{2}+(R-r)^{2}=(R+r)^{2}$ $R^{2}+R^{2}-2Rr+r^{2}=R^{2}+2Rr+r^{2}$ $R^{2}-2Rr=2Rr$ $R^{2}=4Rr$ $R=4r$ $r=\frac{1}{4}R$ Odp.: Promie艅 mniejszego okr臋gu wynosi $\frac{1}{4}R$. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj