Inne, zadanie nr 2585
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
maniek83 post贸w: 4 |  2013-02-28 20:34:26 2013-02-28 20:34:26prosze o pomoc zd1 podstawa graniastoslupa prostego jest romb. krotsza przekatna rombu tworzy z krawedzia podstawy kat 60 i ma dlugosc 4 pierwiastki z 3 . dluzsza przekatna graniastoslupa tworzy z dluzsza przekatna rombu kat 60. oblicz objetosc graniastoslupa zd2 podstawa trojkata rownobocznego ABC zawarta jest w prostej y= \frac{3}{4} x + 1 a wierzcholek C=(-1,4) wyznacz wspolrzedne wierzcholkow A,B tego trojk膮ta ( ulamek 3/4 x + 1 ni e wiem czy dobrze zapisalem w tym programie) zd3 ksiegarz kupil w hurtowni 20 przewodnikow i 30 map za 1020zl. przewodniki sprzedal z zyskiem 20% a mapy z zyskiem 25% w ten sposob zarobil 240 zl. oblicz w jakiej cenie ksi臋garz kupil w hurtowni przewodniki a w jakiej mapy W jednym temacie maj膮 by膰 co najwy偶ej 3 zadania- patrz REGULAMIN Wiadomo艣膰 by艂a modyfikowana 2013-03-01 19:29:00 przez irena |
zorro post贸w: 106 |  2013-03-06 18:23:43 2013-03-06 18:23:431. Przyjmijmy oznaczenia: $p_{1}=4\sqrt{3}$ - kr贸tsza przek膮tna r膮bu $p_{2} $ - d艂u偶sza przek膮tna r膮bu $h $ - wysoko艣膰 graniastos艂upa Aby policzy膰 obj臋to艣膰 trzeba zna膰 pole podstawy i wysoko艣膰. Zacznijmy od podstawy czyli liczymy pole rombu: Skoro kr贸tsza przek膮tna tworzy k膮t 60 stopni z kraw臋dzi膮 wi臋c wiedz膮c, 偶e w rombie przek膮tne przecinaj膮 si臋 pod k膮tem prostym widzimy, 偶e: $\frac{\frac{p_{2}}{2}}{\frac{p_{1}}{2}}=tg(60^{o})$ $p_{2}=p_{1}*\sqrt{3}=4\sqrt{3}\sqrt{3}=4*3=12$ Ze wzoru na pole rombu przy znajomo艣ci przek膮tnych obliczamy pole podstawy: $P=\frac{1}{2}p_{1}p_{2}=\frac{1}{2}*4\sqrt{3}*12=24\sqrt{3}$ Teraz znajdujemy wysoko艣膰 h: Skoro przek膮tna d艂u偶sza graniastos艂upa tworzy 60 stopni z d艂u偶sz膮 przek膮tn膮 rombu to: $\frac{h}{p_{2}}=tg(60^{o})$ $h=p_{2}*\sqrt{3}=12\sqrt{3}$ Teraz ju偶 mo偶na policzy膰 obj臋to艣膰: $V=P*h=24\sqrt{3}*12\sqrt{3}=24*12*3=864$ |
zorro post贸w: 106 |  2013-03-06 22:31:35 2013-03-06 22:31:352. 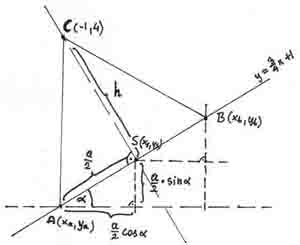 Aby znale藕膰 wsp贸艂rz臋dne punkt贸w A i B wystarczy od 艣rodka podstawy S od艂o偶y膰 wzd艂贸偶 danej prostej odleg艂o艣膰 $\frac{a}{2}$ w obu kierunkach. Oznacza to ,偶e: $x_{a}=x_{s}-\frac{a}{2}cos(\alpha)$ - rzut poziomy po艂owy podstawy $y_{a}=y_{s}-\frac{a}{2}sin(\alpha)$ - analogicznie w pionie Podobnie b臋dzie: $x_{b}=x_{s}+\frac{a}{2}cos(\alpha)$ $y_{b}=y_{s}+\frac{a}{2}sin(\alpha)$ Pozostaje odnale藕膰 wsp贸艂rz臋dne 艣rodka i d艂ugo艣膰 podstawy: Prosta wyznaczona przez punkty C i S jest prostopad艂a do zadanej prostej, wi臋c: $l_{CS}: y=-\frac{4}{3}x+k$ sta艂膮 k znajdujemy wiedz膮c, 偶e $C\in l_{CS}$. Wsp贸艂rz臋dne C(-1,4) spe艂niaj膮 to r贸wnanie: $4=-\frac{4}{3}(-1)+k \Rightarrow k=\frac{8}{3}$ $l_{CS}: y=-\frac{4}{3}x+\frac{8}{3}$ Obie proste przecinaj膮 si臋 w punkcie $S(x_{s},y_{s})$ Wsp贸艂rz臋dne te znajdujemy rozwi膮zuj膮c uk艂ad r贸wna艅: $\left\{\begin{matrix} y_{s}=\frac{3}{4}x_{s}+1 \\ y_{s}=-\frac{4}{3}x_{s}+\frac{8}{3} \end{matrix}\right.$ St膮d: $\left\{\begin{matrix} x_{s}=\frac{4}{5} \\ y{s}=\frac{8}{5} \end{matrix}\right.$ Wysoko艣膰 tr贸jk膮ta b臋dzie r贸wna odleg艂o艣ci |CS| $h=|CS|=\sqrt{(\frac{4}{5}+1)^{2}+(\frac{8}{5}-4)^{2}}=3$ Bok i wysoko艣膰 w tr贸jk膮cie r贸wnobocznym 艂膮czy zale偶no艣膰: $h=a\frac{\sqrt{3}}{2} \Rightarrow a=h\frac{2\sqrt{3}}{3}=2\sqrt{3}$ Szukamy teraz $sin(\alpha) i cos(\alpha)$ Wiemy, 偶e wsp贸艂czynnik kierunkowy prostej $tg(\alpha)=\frac{3}{4}$ Przekszta艂camy wz贸r $tg(\alpha)=\frac{sin(\alpha)}{cos(\alpha)}$ $sin^{2}(\alpha)=tg^{2}(\alpha)cos^{2}(\alpha)=tg^{2}(\alpha)(1-sin^{2}(\alpha))$ st膮d: $sin^{2}(\alpha)=\frac{tg^{2}(\alpha)}{1+tg^{2}(\alpha)}=\frac{(\frac{3}{4})^2}{1+(\frac{3}{4})^{2}}=\frac{9}{25}$ Z jedynki trygonometrycznej: $cos^{2}(\alpha)=1-sin^{2}(\alpha)=1-\frac{9}{25}=\frac{16}{25}$ Poniewa偶 k膮t $\alpha$ jest ostry wi臋c sinus i cosinus b臋d膮 dodatnie: $sin(\alpha)=\frac{3}{5}$ $cos(\alpha)=\frac{4}{5}$ Obliczamy teraz wsp贸艂rz臋dne punkt贸w A i B: $x_{a}=x_{s}-\frac{a}{2}cos(\alpha)=\frac{4}{5}-\sqrt{3}\frac{4}{5}=\frac{4}{5}(1-\sqrt{3})$ $y_{a}=y_{s}-\frac{a}{2}sin(\alpha)=\frac{8}{5}-\sqrt{3}\frac{3}{5}=\frac{1}{5}(8-3\sqrt{3})$ $x_{b}=x_{s}+\frac{a}{2}cos(\alpha)=\frac{4}{5}+\sqrt{3}\frac{4}{5}=\frac{4}{5}(1+\sqrt{3})$ $y_{b}=y_{s}+\frac{a}{2}sin(\alpha)=\frac{8}{5}+\sqrt{3}\frac{3}{5}=\frac{1}{5}(8+3\sqrt{3})$ Szukane punkty: $A(\frac{4}{5}(1-\sqrt{3}),\frac{1}{5}(8-3\sqrt{3}))$ $B(\frac{4}{5}(1+\sqrt{3}),\frac{1}{5}(8+3\sqrt{3}))$ |
zorro post贸w: 106 |  2013-03-06 22:55:23 2013-03-06 22:55:233. p - cena pierwotna przewodnika m - cena pierwotna mapy 1.2p - cena przewodnika z zyskiem 20% 1.25m - cena mapy z zyskiem 25% 1020+240=1260 - kwota sprzeda偶y wszystkich map i przewodnik贸w z zyskem Z tre艣ci wynika, 偶e: $20p+30m=1020$ oraz $20*1.2p+30*1.25m=1260$ Upraszczaj膮c te r贸wnania mamy uk艂ad: $\left\{\begin{matrix} 2p+3m=102 \\ 16p+25m=840 \end{matrix}\right.$ pierwsze mno偶ymy przez (-8)i dodajemy stronami: $\left\{\begin{matrix}-16p-24m=-816 \\ 16p+25m=840 \end{matrix}\right.$ $m=24$ czyli: $2p+3*24=102$ $p=15$ Przewodnik kosztowa艂 oryginalnie 15z艂 za szt., a mapa 24z艂 za szt. Za wszystkie przewodniki ksi臋garz zap艂aci艂 20*15 = 300 z艂, a za wszystkie mapy 30*24=720z艂. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj