Stereometria, zadanie nr 2608
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
maciek6688 post贸w: 1 |  2013-03-04 17:28:26Mam dane alfa, beta i gamma i boki a i b trapezu kt贸ry to obracam wzgl臋dem prostej jak na rysunku. Mam policzy膰 Obj臋to艣膰 i Pole. Potrzebuj臋 jaki艣 wskaz贸wek bo utkn膮艂em.  |
zorro post贸w: 106 | 2013-03-13 07:09:20 Mo偶e to pomo偶e. 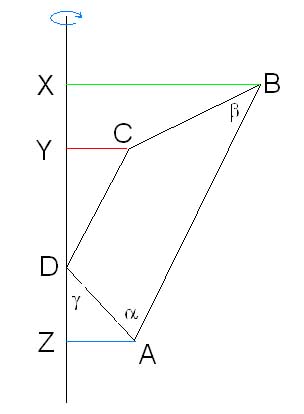 B臋d膮 sumy i r贸偶nice samych sto偶k贸w. Wiadomo艣膰 by艂a modyfikowana 2013-03-13 18:24:05 przez zorro |
zorro post贸w: 106 | 2013-03-13 18:36:28 Oznaczenia: Dane: $a,\space b,\space\alpha,\space\beta,\space\gamma$ |AB|=a |DC|=b Potrzebne do oblicze艅 |DA|=c |CB|=d |ZA|=$r_{1}$ |YC|=$r_{2}$ |XB|=$r_{3}$ |DZ|=$h_{1}$ |DY|=$h_{2}$ |XY|=$h_{3}$ Szukamy dla powsta艂ej bry艂y obrotowej: $V_{ABCD}=?$ $S_{ABCD}=?$ |
zorro post贸w: 106 | 2013-03-13 19:23:32 Zaczynamy od obliczenia trapezu. Brakuje nam bok贸w c i d. W tym trapezie mamy: $\left\{\begin{matrix} a=c*cos\alpha+b+d*cos\beta\\ c*sin\alpha=d*sin\beta \end{matrix}\right.$ $\left\{\begin{matrix} c*cos\alpha+d*cos\beta=a-b \\ c*sin\alpha-d*sin\beta=0 \end{matrix}\right.$ Stosuj膮c metod臋 wyznacznik贸w, (lub licz膮c przez podstawianie)wyliczamy: $c=\frac{(a-b)sin\beta}{sin(\alpha+\beta)}$ $d=\frac{(a-b)sin\alpha}{sin(\alpha+\beta)}$ Teraz: $r_{1}=c*sin\gamma$ $h_{1}=c*cos\gamma$ $\gamma+(90^{o}-\alpha)+90^{o}+\angle YDC=180^{o}$ $\angle YDC=\alpha-\gamma$ $r_{2}=b*sin(\alpha-\gamma)$ $h_{2}=b*cos(\alpha-\gamma)$ $\angle XBC=90^{o}-[\beta+(\alpha-\gamma)]$ $\angle XBC=90^{o}-(\alpha+\beta-\gamma)$ $r_{3}=r_{2}+d*cos(90^{o}-(\alpha+\beta-\gamma))$ $r_{3}=r_{2}+d*sin(\alpha+\beta-\gamma)$ $h_{3}=d*sin(90^{o}-(\alpha+\beta-\gamma))$ $h_{3}=d*cos(\alpha+\beta-\gamma)$ Przyjmijmy te偶 pomocniczo: $H=h_{1}+h_{2}+h_{3}$ Wszystkie te warto艣ci mamy ju偶 policzone wi臋c czas przyst膮pi膰 do sedna: |
zorro post贸w: 106 | 2013-03-13 20:09:04 $V_{ABCD}=V_{XBAZ}-V_{XBCY}-V_{YCD}-V_{ZAD}$ $V_{XBAZ}$ obliczamy wiedz膮c, 偶e jest to sto偶ek 艣ci臋ty. wysoko艣膰 = $H$ promie艅 ma艂y = $r_{1}$ promie艅 du偶y =$r_{3}$ tworz膮ca = $a$ $V_{XBAZ}=\frac{1}{3}\pi*H*\frac{(r_{3}-r_{1})^{3}}{r_{3}-r{1}}$ Podobnie liczymy $V_{XBCY}$ wysoko艣膰 = $h_{3}$ promie艅 ma艂y = $r_{2}$ promie艅 du偶y =$r_{3}$ tworz膮ca =$d$ $V_{XBCY}=\frac{1}{3}\pi*h_{3}*\frac{(r_{3}-r_{2})^{3}}{r_{3}-r{2}}$ Pozosta艂y zwyk艂e sto偶ki $V_{YCD}$ wysoko艣膰 =$h_{2}$ promie艅 =$r_{2}$ tworz膮ca = $b$ $V_{YCD}=\frac{1}{3}\pi*h_{2}*r_{2}^2$ $V_{ZAD}$ wysoko艣膰 =$h_{1}$ promie艅 =$r_{1}$ tworz膮ca = $c$ $V_{ZAD}=\frac{1}{3}\pi*h_{1}*r_{1}^2$ Pozostaje podstawi膰 wyliczone poprzednio warto艣ci i poupraszcza膰 co si臋 da. Zostawmy to zakonnikom. Powierzchnia: $S_{ABCD}=Pb_{XBAZ}+Pb_{XBCY}+Pb_{YCD}+Pb_{ZAD}$ $Pb_{XBAZ}$ to pole powierzchni bocznej sto偶ka 艣ci臋tego Parametry tego sto偶ka - jak wy偶ej. $Pb_{XBAZ}=\pi*a*(r_{3}+r_{1})$ Podobnie $Pb_{XBCY}$ to pole powierzchni bocznej sto偶ka 艣ci臋tego Parametry tego sto偶ka - jak wy偶ej. $Pb_{XBCY}=\pi*d*(r_{3}+r_{2})$ Dalej mamy pola pow. bocznej zwyk艂ych sto偶k贸w $Pb_{YCD}=\pi*b*r_{2}$ $Pb_{YCD}=\pi*c*r_{1}$ I to by by艂o na tyle. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj