Stereometria, zadanie nr 3162
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
kokabango post贸w: 144 |  2013-10-05 20:05:47zad 1. kraw臋d藕 podstawy graniastos艂upa prawid艂owego czworok膮tnego ma d艂ugo艣膰 5 cm. oblicz pole powierzchni ca艂kowitej tego graniastos艂upa , je艣li przek膮tna jego 艣ciany bocznej tworzy: b) z kraw臋dzi膮 boczna kat 30 stopni c) z przek膮tna graniastos艂upa kat 30 stopni bardzo prosz臋 o pomoc i dok艂adne obliczenia do zad 1 , bo mam k艂opot , z g贸ry dzi臋kuje . Karola |
agus post贸w: 2387 | 2013-10-05 20:51:32 a-kraw臋d藕 podstawy b-kraw臋d藕 boczna P=$2a^{2}+4ab$ b) ctg $30^{0}=\frac{b}{a}$ $\sqrt{3}=\frac{b}{5}$ b=$5\sqrt{3}$ P=50+100$\sqrt{3}$ |
agus post贸w: 2387 | 2013-10-05 20:57:58 c) p-przek膮tna 艣ciany bocznej ctg $30^{0}=\frac{p}{a}$ $\sqrt{3}=\frac{p}{5}$ p=5$\sqrt{3}$ $b^{2}=p^{2}-a^{2}$ b=$\sqrt{(5\sqrt{3})^{2}-5^{2}}=\sqrt{75-25}=\sqrt{50}=5\sqrt{2}$ P=50+100$\sqrt{2}$ |
abcdefgh post贸w: 1255 | 2013-10-05 20:59:41 zad.1 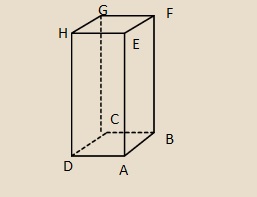 b) $tg(30^{o})=\frac{AB}{EA}=\frac{5}{x}$ $x=5\sqrt{3}$ $Pc=2*5^2+4*5*5\sqrt{3}=50+100\sqrt{3}$ c) $tg(30^{o})=\frac{5}{AF}$ $\sqrt{3}/3*AF=5$ $AF=5\sqrt{3}$ $HD^2=5\sqrt{3}^2-5^2=5\sqrt{2}$ Pc=$50+100\sqrt{2}$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj