Trygonometria, zadanie nr 6312
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
marta1604 post贸w: 1 |  2020-04-15 12:39:51Witam, mam problem z dwoma r贸wnaniami. 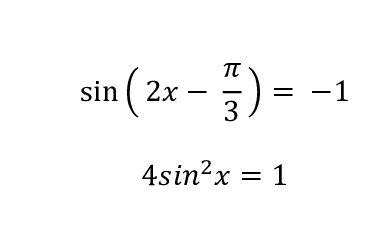 Z g贸ry dzi臋kuj臋 za pomoc! Wiadomo艣膰 by艂a modyfikowana 2020-04-15 12:54:20 przez marta1604 |
chiacynt post贸w: 749 | 2020-04-15 16:25:43 $ \sin\left( 2x -\frac{\pi}{3}\right) = -1 $ Jak zajrzymy do podr臋cznika i narysujemy wykres funkcji sinus (sinusoid臋), to zauwa偶ymy, 偶e przyjmuje ona warto艣膰 $ -1 $ w punktach $-\frac{\pi}{2}, - \frac{\pi}{2} 2k\cdot\pi, \ \ k\in Z.$ St膮d otrzymujemy $ \sin\left( 2x -\frac{\pi}{3}\right) = -1 $ $ 2x - \frac{\pi}{3} = -\frac{\pi}{2} + 2k\cdot \pi $ $ 2x = -\frac{1}{2}\pi + \frac{1}{3}\pi+ 2k\cdot \pi $ $ 2x = -\frac{1}{6}\pi + 2k\cdot \pi $ $ x = -\frac{1}{12}\pi + k \cdot \pi.$ $ 4\sin^2(x) = 1 $ $ \sin^2(x) = \frac{1}{4}$ $ \sin (x) = -\frac{1}{2} $ lub $ \sin(x) = \frac{1}{2}. $ Prosz臋 rozwi膮za膰 te dwa r贸wnania, pami臋taj膮c, 偶e sinus ma dwa rozwi膮zania $ \alpha, \ \ \pi-\alpha.$ Wiadomo艣膰 by艂a modyfikowana 2020-04-15 16:29:13 przez chiacynt |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj