Algebra, zadanie nr 1623
ostatnie wiadomości | regulamin | latex
| Autor | Zadanie / Rozwiązanie |
| sangwinik postów: 3 |  2013-10-27 22:23:19Znajdź rozwiązania na płaszczyźnie zespolonej: $|\frac{z+i}{z^2+1}|\ge1$ $2\le|iz-5|<3$ Znajdź postać trygonometryczną liczby: $z=1+itg\alpha$ |
| abcdefgh postów: 1255 | 2013-10-27 23:43:46 $|z+i|=|x+iy+i|=|z+i(y+1)|=\sqrt{x^2+(y+1)^2}$ $|z^2+i|=|x^2+2iy+y^2i^2+i|=|x^2-y^2+i(2y+1)|=\sqrt{x^2+y^2+(2y+1)^2}$ $\sqrt{\frac{x^2+(y+1)^2}{x^2+y^2+(2y+1)^2}} \ge 1$ $\sqrt{x^2+(y+1)^2} \ge \sqrt{x^2+y^2+(2y+1)^2} |^2$ $x^2+y^2+2y+1 \ge x^2 +y^2 + 4y^2+4y+1$ $2y+1 \ge 4y^2+4y+1$ $4y^2+2y \le 0$ $y=0 \ v \ y=-0,5$ Wiadomość była modyfikowana 2013-10-28 00:29:10 przez abcdefgh |
| abcdefgh postów: 1255 | 2013-10-28 00:26:20 $2\le|iz-5|<3$ $|iz-5|=|i(x+iy)-5|=|xi+i^2y-5|=|x-y-5|=\sqrt{(x-5)^2+y^2}$ $\sqrt{(x-5)^2+y^2} \ge 2$ $(x-5)^2+y^2 \le 4$ $(x-5)^2+y^2 \ge 9$ 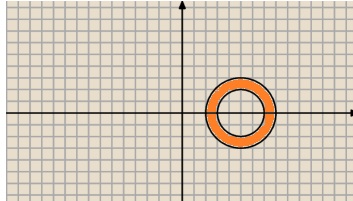 Wiadomość była modyfikowana 2013-10-28 00:33:31 przez abcdefgh |
| strony: 1 | |
Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj