Geometria, zadanie nr 191
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
wenm post贸w: 2 |  2011-11-08 16:49:46Witam serdecznie, mam problem z pewnym zadaniem, chodzi o wyliczenie wsp贸艂rz臋dnych przeci臋cia prostej z okr臋gami. Mam wsp贸艂rz臋dne dw贸ch 艣rodk贸w, odleg艂o艣膰 mi臋dzy jednym a drugim okr臋giem i promienie okr臋g贸w. Szukam wsp贸艂rz臋dnych odcinka le偶膮cego na tej prostej 艂膮cz膮cej okr臋gi. 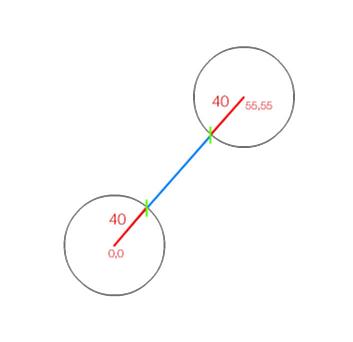 pozdrawiam :) edycja: obrazek za艂adowany zosta艂 na serwer Wiadomo艣膰 by艂a modyfikowana 2011-11-08 21:26:35 przez Mariusz 艢liwi艅ski |
sylwia94z post贸w: 134 | 2011-11-08 21:12:37 |
Mariusz 艢liwi艅ski post贸w: 489 | 2011-11-08 21:20:20 Prosta 艂膮cz膮ca okr臋gi: $y = x$ A, B - ko艅ce odcinka 艂膮cz膮cego okr臋gi. $A = (x_1, y_1)$ $B = (x_2, y_2)$ $x_1 = y_1$ $2{x_1}^2 = 40^2$ ${x_1 = 20\sqrt{2}$ $A = (20\sqrt{2}, 20\sqrt{2})$ $B = (55 - 20\sqrt{2}, 55- 20\sqrt{2})$ |
wenm post贸w: 2 | 2011-11-08 21:48:46 Dzi臋ki wielkie za szybk膮 odpowied藕. Problem jest bardziej z艂o偶ony, okr臋gi mog膮 pojawia膰 si臋 w losowym po艂o偶eniu (zawsze znam x,y 艣rodka ka偶dego z nich oraz promienie i odleg艂o艣ci mi臋dzy 艣rodkami).. Pani Sylwia przyj臋艂a 偶e tr贸jk膮t ma dwa boki r贸wne, a tak nie koniecznie musi by膰. Promienie te偶 mog膮 by膰 dowolne (ale zawsze znane s膮 ich d艂ugo艣ci) Pozdrawiam i jeszcze raz dzi臋ki za odpowiedzi |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj