Analiza matematyczna, zadanie nr 2066

Autor	Zadanie / Rozwiązanie
zamek1320 postów: 1	2014-02-02 19:04:40 Mógł by ktoś pomóc? wiem na temat tego przykładu że wynik =-1... ale obliczenia potrzebne 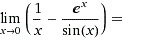Wiadomość była modyfikowana 2014-02-02 19:05:51 przez zamek1320

przyjaciel postów: 4	2014-02-02 23:28:25 $lim_{x \to 0}\left(\frac{1}{x}-\frac{e^x}{\sin x}\right)$ $=lim_{x \to 0}\left(\frac{\sin x- x e^x}{x \sin x}\right)\left[\frac{0}{0}\right]$ $\stackrel{H}=lim_{x \to 0}\left(\frac{\cos x- e^x - x e^x}{ \sin x + x\cos x}\right)\left[\frac{0}{0}\right]$ $\stackrel{H}=lim_{x \to 0}\left(\frac{-\sin x- e^x- e^x - x e^x}{ \cos x + \cos x -x \sin x }\right)= \frac{-2}{2}=-1$ H nad rownoscia oznacza, ze korzystamy z reguly l'hospitala. https://www.facebook.com/pages/Powiernik-żywych

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj