Analiza matematyczna, zadanie nr 2420
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
simaxlion post贸w: 3 |  2014-06-04 15:57:37Witam, mam problem z w艂a艣ciwie raczej prostym zadaniem z II tomu podr臋cznika pan贸w Krysickiego i W艂odarskiego, mianowicie jest to zadanie 4.14 Ot贸偶 chyba nie umiem dobrze dobra膰 granic ca艂kowania, do艣膰, 偶e ca艂y czas wynik nie chce si臋 zgodzi膰 z podanym z ty艂u ksi膮偶ki, czyli 14/3 A oto tre艣膰 zadania, w skr贸cie: Obliczy膰 ca艂k臋 z funkcji f(x,y)= x+2y gdzie obszarem ca艂kowania jest tr贸jk膮t o wierzcho艂kach A(0,0), B(2,2), C(-1,1). Bardzo prosi艂bym o pomoc, pr贸bowa艂em podstawia膰 granice na r贸偶ne sposoby, ale ca艂y czas nie wychodzi :/ |
abcdefgh post贸w: 1255 | 2014-06-05 20:09:12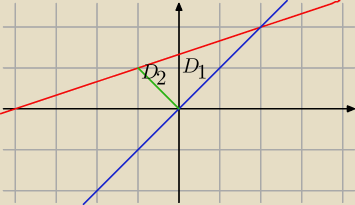 Obszar $D_{1}$ $0 \le x \le 2$ $x \le y \le \frac{x+4}{3}$ wyliczamy z pkt B i C $\int_{0}^{2} \int_{x}^{\frac{x+4}{3}} (x+2y)dydx=\int_{0}^{2}(xy+y^2)|_{x}^{\frac{x+4}{3}}dx =$ $\int_{0}^{2}(\frac{1}{3}x^2+\frac{4}{3}x+\frac{1}{9}x^2+\frac{8}{9}x-x^2-x^2)dx=\int_{0}^{2}(\frac{14}{9}x^2+\frac{20}{9}x+\frac{16}{9})dx=$ $(\frac{14}{9}\frac{x^3}{3}+\frac{20}{9}\frac{x^2}{2}+\frac{16}{9}x)|_{0}^{2}=\frac{-14*8}{27}+\frac{20*4}{18}+\frac{16*2}{9}-0=3\frac{23}{27}$ Teraz po $D_{2}$ $-1 \le x \le 0$ $-x \le y \le \frac{x+4}{3}$ $\int_{-1}^{0} \int_{-x}^{\frac{x+4}{3}} (x+2y)dydx=\int_{-1}^{0}(xy+y^2)|_{-x}^{\frac{x+4}{3}}dx =$ $\int_{-1}^{0}(\frac{1}{3}x^2+\frac{4}{3}x+\frac{1}{9}x^2+\frac{8}{9}x+x^2-x^2)dx=\int_{-1}^{0}(\frac{4}{9}x^2+\frac{20}{9}x+\frac{16}{9})dx=$ $(\frac{4}{9}\frac{x^3}{3}+\frac{20}{9}\frac{x^2}{2}+\frac{16}{9}x)|_{-1}^{0}=\frac{4}{27}-\frac{20}{18}+\frac{16}{9}=\frac{22}{27}$ $\int_{D_{1}}\int f(x,y)+\int_{D_{2}}\int f(x,y)=3\frac{23}{27}+\frac{22}{27}=4\frac{2}{3}$ |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj