Analiza matematyczna, zadanie nr 2440

Autor	Zadanie / Rozwiązanie
rambo postów: 19	2014-06-11 10:56:50 Witam, Bardzo proszę o pomoc w rozwiązaniu całki podwójnej po obszarze D ograniczonej podanymi krzywymi: $y-x-2=0$ $y-x^2+2x-2=0$ całka podwójna: $\int \int_{D}^{} xdxdy$

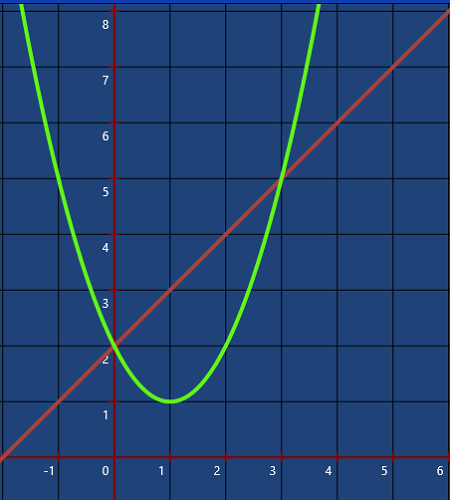abcdefgh postów: 1255	2014-06-16 11:44:08 wzyaczamy x: $x+2=x^2-2x+2$ $x^2-3x=0 \ \ \Rightarrow \ \ x(x-3) \ \ \Rightarrow \ \ x=0 \ \wedge \ x=3$ $x\in[0,3]$ $y \in [x^2-2x+2;x+2]$ $\int_{0}^{3}\int_{x^2-2x+2}^{x+2}x d(y,x)=\int_{0}^{3} (\frac{x^2}{x})\|_{x^2-2x+2}^{x+2}dy=\int_{0}^{3} \frac{(x+2)^2}{2}-\frac{(x^2-2x+2)^2}{2} dy $ $\int_{0}^{3}\frac{1}{2}(-x^4+4 x^3-7 x^2+12 x)\|_{0}^{3}=\frac{1}{2}(\frac{-x^5}{5}+4\frac{x^4}{4}-7\frac{x^3}{3}+12\frac{x^2}{2})\|_{0}^{3}$ $\frac{1}{2}(-48,6+81-189+54)=23,4$

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj