Algebra, zadanie nr 2851

Autor	Zadanie / Rozwiązanie
273358karolina postów: 1	2014-11-27 13:43:33 Potrzebuje pomocy w narysowaniu i wyznaczeniu dziedziny funkcji: a) f(x)=5+log6 stopnia z x b)f(x)= 6-5^(3x+8) c) f(x)= pierwiastek x+1 dla x R+ 3x dla x należy do R/R+ d) f(x)= 2x+1/x-2 dla x\neq 2 1 dla x=2 e) f(x)=2^(x^2-1) f) f(x)= 7^(3+logx) g) f(x)= e^(x^3+5) h)f(x)=log^2 z x

abcdefgh postów: 1255	2014-11-27 16:49:05 a) $D=(0,+\infty)$ 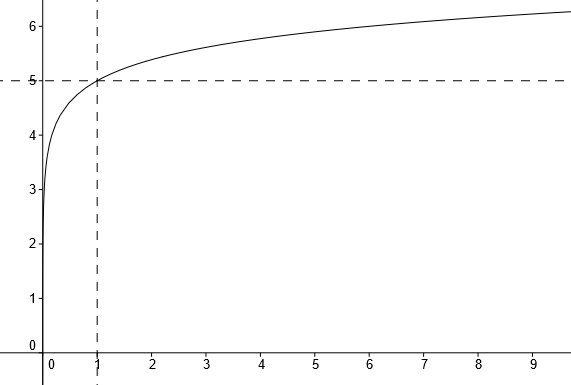b)$f(x)= 6-5^{3x+8}$ $D=\mathbb{R}$ 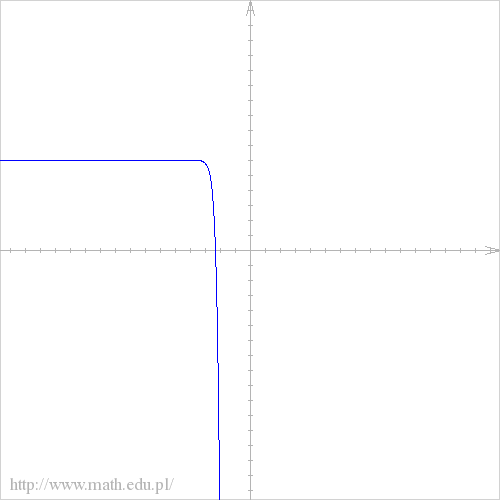c)$f(x)= \left\{\begin{matrix} \sqrt{x+1}, \ gdy \ x \in \mathbb{R_{+}} \\ 3x , \ gdy \ x \in R\backslash R_{+}\end{matrix}\right.$ $D=\mathbb{R}\backslash \{0\}$ 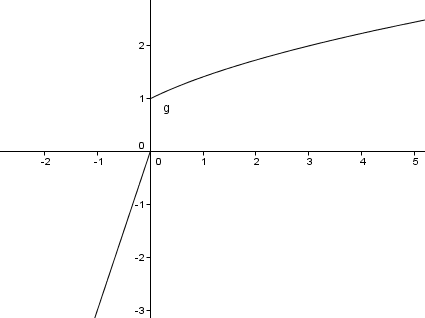d) $f(x)= \left\{\begin{matrix} \frac{2x+1}{x-2}, \ gdy \ x \neq 2 \\ 1 , \ gdy \ x=2 \end{matrix}\right.$ 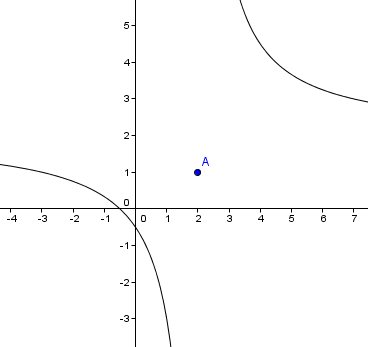e)$ f(x)=2^{x^2-1}$ $D=\mathbb{R}$ 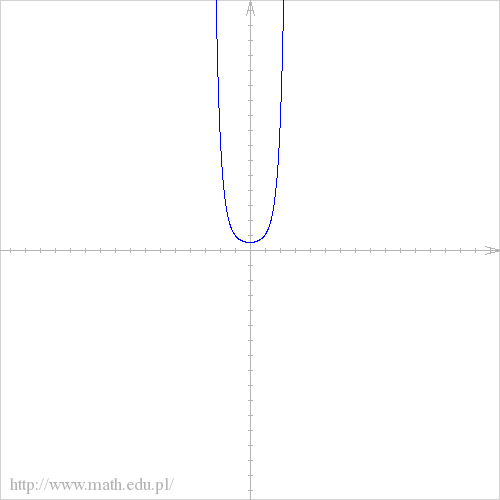f) $f(x)= 7^(3+logx)$ $D=(0,+\infty)$ 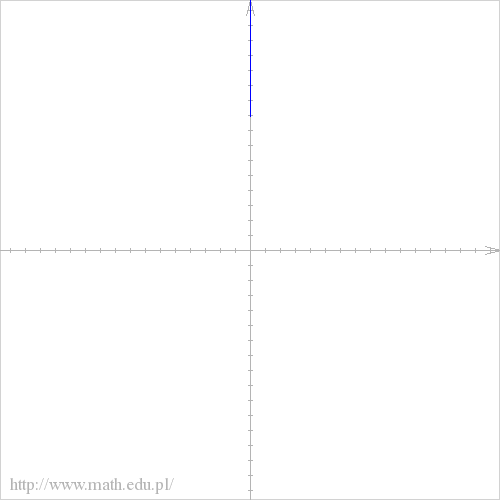g)$f(x)= e^{x^3+5}$ $D=\mathbb{R}$ 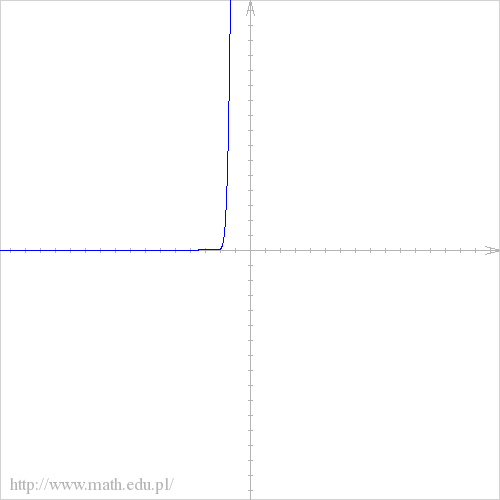h) $f(x)=(\log(x))^2 $ $D=(0,+\infty)$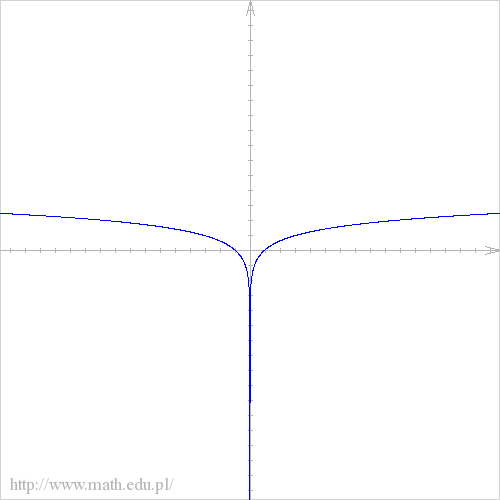

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj