Analiza matematyczna, zadanie nr 2948

Autor	Zadanie / Rozwiązanie
geometria postów: 865	2014-12-30 18:30:51 Przedstawic calke $\sqrt{x^{2}+y^{2}}$ we wspolrzednych biegunowych, ktora jest w granicach 0$\le$x$\le$8, 0$\le$y$\le$$\sqrt{-x^{2}+8x}$ x=rcos$\theta$ y=rsin$\theta$ rsin$\theta$$\le$$\sqrt{-r^{2}{cos}^{2}\theta+8rcos\theta}$ /$ {()}^{2}$ r$\le$8cos$\theta$ a jak wyliczyc kat? tzn. ...$\le$$\theta$$\le$...

abcdefgh postów: 1255	2014-12-31 00:59:02 Najpier rysunek: 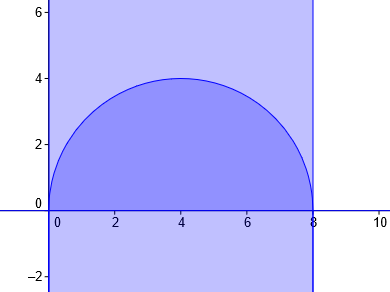$0 \le \alpha \le \frac{\pi}{2}$ $y \le \sqrt{8x-x^2} \|^2$ $y^2+x^2-8x \le 0$ $x=rcos \alpha$ $y=rsin \alpha$ $r^2(cos^2 \alpha + sin^2 \alpha ) -8rcos \alpha \le 0$ $r^2 - 8rcos \alpha \le 0 $ $r(r-8cos \alpha) \le 0$ $r=0 \ \ \ r=8cos \alpha$ $0 \le r \le 8cos \alpha$ $\int_{0}^{\frac{\pi}{2}} \int_{0}^{8cos \alpha} r^2 d(r, \alpha)$

strony: 1

Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj