Logika, zadanie nr 2973
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
cmdmaniek post贸w: 2 |  2015-01-05 11:59:42Witam :) Czy kto艣 potrafi wyt艂umaczy膰, jak podane ni偶ej formu艂, udowodni膰 za pomoc膮 metody dowodu nie wprost 偶e s膮 one tautologi膮 ? <a href=\"http://www.pl.image-share.com\" target=\"_blank\"><img src=\"http://www.pl.image-share.com/upload/366/84.jpg\" border=\"0\" alt=\"free image hosting\"></a> Z g贸ry dzi臋ki |
cmdmaniek post贸w: 2 | 2015-01-05 12:03:14 |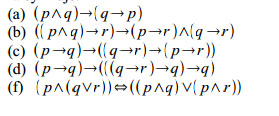
abcdefgh post贸w: 1255 | 2015-01-05 14:43:49 a) metoda nie wprost $w[(p\wedge g ) \Rightarrow (q \Rightarrow p)]=0$ $\left\{\begin{matrix} w[(p\wedge g )]=1 \\ w[(q \Rightarrow p)]=0 \end{matrix}\right.$ $w(p\wedge g)=1$ $w(p)=1$ $w(q)=1$ $(q \Rightarrow p)]=0$ $w(q)=1$ $w(p)=0$ sprzeczno艣c, wi臋c jest tautologi膮 |
abcdefgh post贸w: 1255 | 2015-01-05 14:59:21 b) $w[(p \wedge q)] \Rightarrow r ]=1$ $w[(p \Rightarrow q) \wedge (q \Rightarrow r)]=0$ $w[(p \wedge q)] \Rightarrow r ]=1$ 1.$w[(p \wedge q)] = 1$ $w(p)=1=w(q)$ $w(r)=1$ $w[(p \Rightarrow q)=1$ $(q \Rightarrow r)]=1$ sprzeczno艣膰 2. $w[(p \wedge q)] = 0$ $w(p)=1 =w(q)$ $w(r)=0$ $w[(p \Rightarrow q)=1$ $(q \Rightarrow r)]=0$ to nie jest tautologia Wiadomo艣膰 by艂a modyfikowana 2015-01-05 15:22:02 przez abcdefgh |
abcdefgh post贸w: 1255 | 2015-01-05 16:00:03 c) tautologia d) tautologia e) tautologia |
abcdefgh post贸w: 1255 | 2015-01-05 16:00:04 c) tautologia d) tautologia e) tautologia |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj