Algebra, zadanie nr 3174
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
ketaminehigh post贸w: 4 |  2015-02-02 23:14:22Niech $f:\mathbb{R}\rightarrow\mathbb{R}$ b臋dzie funkcj膮 okre艣lon膮 wzorem: $ f(x)= \left\{\begin{array}{rcl} x^2-1& dla& x\in(-\infty,1 )\\ x-1 & dla& x\in[1,2)\\ 3-x & dla& x\in[2,\infty) \end{array} \right.$ a) Sprawdzi膰, czy f jest r贸偶nowarto艣ciowa i czy jest \"na\" $\mathbb{R}$ b) Wyznaczy膰 $f((-1,3))$, $f^{-1}([1,3))$ oraz $ f^{-1}((-1, 0))$ |
abcdefgh post贸w: 1255 | 2015-02-03 01:08:02 a) nie jest r贸偶nowarto艣ciwowa $2 \neq -\sqrt{2}$ f(2)=1=f(-\sqrt{2}) albo $-1 \neq 1 \neq 3$ f(-1)=0=f(1)=f(3) zbi贸r warto艣ci funkcji oraz przeciwdziedzina s膮 sobie r贸wne, czyli funkcja jest surjekcj膮. |
abcdefgh post贸w: 1255 | 2015-02-03 01:20:07 |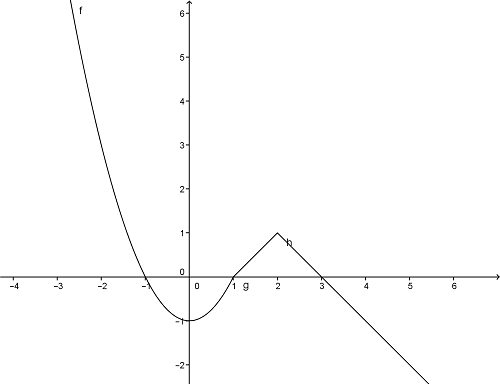
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj