Statystyka, zadanie nr 4082
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
rutek2121 post贸w: 8 |  2016-01-10 20:03:25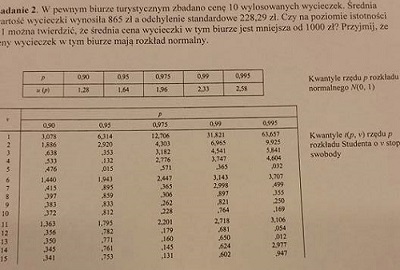 A czy to si臋 robi analogicznie? Mam problem, poniewa偶, poziom istotno艣ci jest r贸wny 1. |
janusz78 post贸w: 820 | 2016-01-10 20:31:23 To zadanie nie robi analogicznie, bo dotyczy ono weryfikacji hipotezy 艣redniej. Przyjmujemy wsp贸艂czynnik istotno艣ci testu $\alpha = 0$ |
rutek2121 post贸w: 8 | 2016-01-10 20:41:11 A czy nie nadu偶yj臋 Pa艅skiej 偶yczliwo艣ci prosz膮c kolejny raz o pomoc? |
janusz78 post贸w: 820 | 2016-01-10 21:20:45 Hipotezy: $ H_{0}: m_{0} = 1000 $ z艂; $H_{1}: m_{0} < 1000 $ z艂. Statystyka testowa: $ Z_{n}= \frac{X_{n}- m_{0}}{S_{n}}\sqrt{n-1}.$ Statystyka, ta przy prawdziwo艣ci hipotezy $ H_{0}$ ma rozk艂ad Studenta z $ (n-1) $ stopniami swobody. Program R Warto艣膰 statystyki dla danych z zadania > n =10 > x10 = 865 > s10= 228.29 > m0= 1000 > z10= ((x10-m0)/s10)*sqrt(n-1) > z10 [1] -1.774059 Znajdujemy kwantyl rz臋du $ \alpha = 0 $ rozk艂adu Studenta z $ n-1 = 10-1 =9$stopniami swobody. qalpha = qt(0, 9) > qalpha [1] -Inf Lewostronny obszar krytyczny testu $ K= (-\infty, 0 >.$ Warto艣膰 statystyki $ z_{10}\approx -1,77$ nale偶y do obszaru krytycznego $ K.$ Hipotez臋 $ H_{0} $ odrzucamy na rzecz hipotezy alternatywnej $ H_{1}.$ Na poziomie istotno艣ci r贸wnym 1 mo偶na twierdzi膰, 偶e 艣rednia cena wycieczki w tym biurze jest mniejsza od $ 1000 $ z艂. |
| strony: 1 2 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj