Geometria, zadanie nr 5335
ostatnie wiadomo┼Ťci | regulamin | latex
| Autor | Zadanie / Rozwi─ůzanie |
geometria post├│w: 865 |  2017-02-15 22:55:46 2017-02-15 22:55:46Kwadraty z rysunku maj─ů wsp├│lny wierzcho┼éek A, a punkt M jest ┼Ťrodkiem odcinka PU. Poka┼╝, ┼╝e AM jest po┼éow─ů RS. 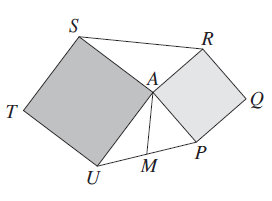 Z tresci zadania wiemy, ze $\angle SAU=\angle RAP=90^{\circ}$ oraz $|UM|=|PM|$. Niech kat $UAP=\alpha$, a kat $RAS=\beta$. Wowczas $\alpha+\beta=180^{\circ}$. Co jeszcze mozna wymyslec? |
tumor post├│w: 8070 |  2017-02-15 23:05:46 2017-02-15 23:05:46Dorysuj punkt X tak, ┼╝eby PAUX by┼é r├│wnoleg┼éobokiem. Uzasadnij, dlaczego przek─ůtna AX jest taka jak SR. |
| strony: 1 | |
Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj