Analiza matematyczna, zadanie nr 5340
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
geometria post贸w: 865 |  2017-02-17 11:36:20Filip w czasie 10-godzinnej wycieczki spacerowa艂 wzd艂u偶 prostej AB. Jego w臋dr贸wk臋 przedstawia poni偶szy wykres funkcji f, ukazuj膮cy pozycj臋 Filipa w zale偶no艣ci od czasu. (Pozycja jest okre艣lana jako odleg艂o艣膰 od punktu A.) 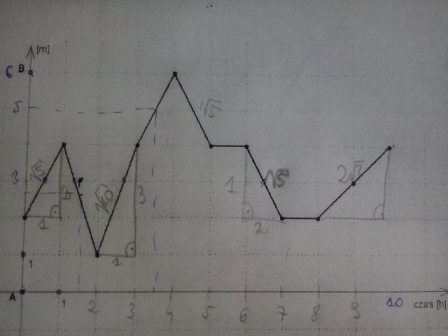 a) Podaj f (1), f (1,5), f (3,5), czyli podaj pozycj臋 Filipa po: godzinie, p贸艂torej godziny, trzech i p贸艂 godzinach od startu. b) W jakiej odleg艂o艣ci od startu Filip zako艅czy艂 w臋dr贸wk臋? c) Ile czasu zaj臋艂y mu odpoczynki na trasie? d) Ile razy Filip przechodzi艂 przez 艣rodek odcinka AB? W kt贸rej godzinie wycieczki? e) W kt贸rej godzinie przeby艂 najwi臋kszy dystans? f) Ile metr贸w przeby艂 w czasie ca艂ej wycieczki? g) Po jakim czasie osi膮gn膮艂 p贸艂metek (tzn. po jakim czasie przeby艂 po艂ow臋 ca艂ego dystansu w臋dr贸wki)? h) Jak d艂ugo by艂 w odleg艂o艣ci nie wi臋kszej ni偶 jeden metr od punktu B? i) Jak d艂ugo by艂 w odleg艂o艣ci wi臋kszej ni偶 jeden metr od punktu startu? a) f(1)=4; f(1,5)=2,5; f(3,5)=5 b) 2m c) 2h d) przechodzil 5 razy; 0,5h; 1,5h; 2,5h; 6,5h; 9h. e) miedzy 1 a 2 oraz 2 a 3; Czy w 2h i 3h? f) ($4\sqrt{5}+2\sqrt{10}+2\sqrt{2}$) m g) ? h) 1h i) 6h Ktore sa dobrze, a ktore nie? |
tumor post贸w: 8070 | 2017-02-17 12:12:04 Je艣li Filip zachowuje jednostajn膮 pr臋dko艣膰 przez godzin臋 i w tym czasie przemierza 2 metry, to jest 艣limakiem. e) 艂adniej po polsku powiedzie膰, 偶e w drugiej godzinie lub w trzeciej godzinie, ale mo偶na powiedzie膰, 偶e mi臋dzy T=1h a T=2h lub mi臋dzy T=2h a T=3h. f) chyba 偶artujesz. g) po艂apiesz si臋, jak Ci minie to dziwne, co robisz w f) i) mo偶esz mi to rozpisa膰? |
geometria post贸w: 865 | 2017-02-17 12:31:00 1. Miedzy 5h a 6h Filip znajduje sie caly czas na pozycji 4m, czyli przez ta godzine stoi w miejscu tak? 2. Czym jest np. $\sqrt{5}$ w pierwszej godzinie? Wiadomo艣膰 by艂a modyfikowana 2017-02-17 12:40:14 przez geometria |
tumor post贸w: 8070 | 2017-02-17 12:49:13 1. tak. 2. Pierwiastkiem z sumy kwadrat贸w po艂o偶enia i czasu. :) Poj臋cia nie mam. Mam za to takie przypuszczenia, 偶e je艣li w T=0 by艂 w po艂o偶eniu 2m, a w czasie T=1 w po艂o偶eniu 4m, przy czym nie zmienia艂 warto艣ci ani kierunku pr臋dko艣ci w tym przedziale czasu, to pokona艂 4-2=2m, a nie $\sqrt{5}$ |
geometria post贸w: 865 | 2017-02-17 13:17:27 f) wowczas przebyl 2+3+3+2+2+0+2+0+2=16km g) czyli po jakim czasie przeszedl 8km, czyli 2+3+3=8km; po 3 h. i) wystartowal 2m od punktu A; 1/2+1/2+1/2+1/2+1/2+1+1+0+1/2+1=6h, ale nie wiem czy dobrze to rozumiem |
tumor post贸w: 8070 | 2017-02-17 23:55:32 i) wsz臋dzie $\frac{1}{2}$, hm, to mo偶e zadam inne pytanie. Gdy pierwszy raz by艂 powy偶ej metra od punktu startu, to jak d艂ugo to trwa艂o? (Zanim wr贸ci艂 w pobli偶e punktu startu) |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj