Rachunek różniczkowy i całkowy, zadanie nr 6301
ostatnie wiadomości | regulamin | latex
| Autor | Zadanie / Rozwiązanie |
| damian123 postów: 19 |  2020-05-23 21:04:33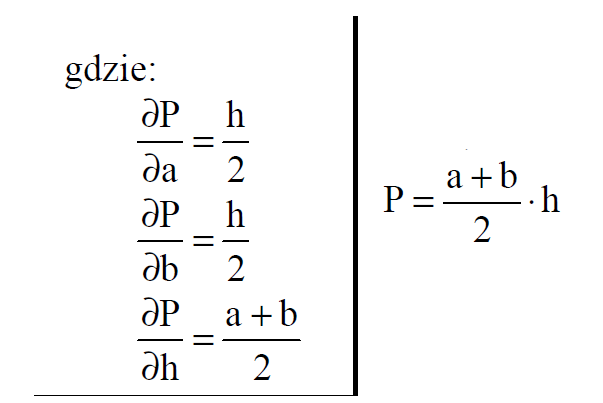 Jak dokonać takie przekształcenie? Proszę o rozpisanie, ponieważ nie ogarniam nic. |
| chiacynt postów: 749 | 2020-05-23 21:26:56 Ze wzoru na pole trapezu obliczamy pochodne cząstkowe względem długości jego podstaw - podstawy $ a $ (ta podstawa wtedy jest zmienną) względem podstawy $ b $ (ta podstawa jest wtedy zmienną) i względem wysokości ( $ h $ jest wtedy zmienną). Obliczamy za każdym razem pochodną funkcji jednej zmiennej przy pozostałych zmiennych będącymi stałymi. |
| damian123 postów: 19 | 2020-05-24 11:19:58 A mógłbyś to pokazać w zapisie? |
| chiacynt postów: 749 | 2020-05-24 12:14:16 Pole trapezu jest funkcją trzech zmiennych (dwóch podstaw i wysokości) $ P(a,b,h) = \frac{a +b}{2}\cdot h = \frac{a}{2}h + \frac{b}{2} h.$ Pochodna cząstkowa względem podstawy $ a $ $ a $ jest zmienną $ \frac{\partial P}{\partial a}(a,b,h) = \left(\frac{a}{2}h\right )'_{|a} + \left( \frac{b}{2}h\right)'|_{|a} = \frac{1}{2}h + 0 = \frac{1}{2}h. $ Pochodna cząstkowa względem podstawy $ b $ $ b $ jest zmienną $ \frac{\partial P}{\partial b}(a,b, h) = \left(\frac{a}{2}h\right)'_{|b} + \left( \frac{b}{2}h\right)'|_{|b} = 0 + \frac{1}{2}h = \frac{1}{2}h. $ Pochodna cząstkowa względem wysokości $ h $ trapezu $ \frac{\partial P}{\partial h}(a,b, h) = \left(\frac{a}{2}h\right)'_{|h} + \left( \frac{b}{2}h\right)'|_{|h} = \frac{a}{2} + \frac{b}{2} = \frac{a+b}{2}. $ Jeśli potrafisz obliczać pochodne funkcji jednej zmiennej, to nie powinieneś mieć trudności z obliczaniem pochodnych cząstkowych funkcji wielu zmiennych. |
| damian123 postów: 19 | 2020-05-24 12:18:27 wielkie dzięki :) |
| strony: 1 | |
Prawo do pisania przysługuje tylko zalogowanym użytkownikom. Zaloguj się lub zarejestruj