Funkcja kotangens

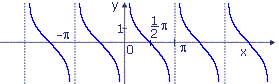
kotangens

y = ctgx

Funkcja kotangens jest określona dla liczb rzeczywistych różnych od liczb postaci
x ≠ kπ, k∈Z
W punktach tych znajdują się asymptoty pionowe wykresu tej funkcji.
D_f = R\ {x:x = kπ, k∈Z}

Wszystkie wartości (przeciwdziedzina) należą do zbioru liczb rzeczywistych
f(X) = R

Kotangens jest funkcją nieparzystą. Oznacza to, że dla każdej liczby należącej do dziedziny funkcji, ctg(-x) = -ctgx.

Kotangens jest funkcją okresową o okresie podstawowym π. Wartości funkcji powtarzają się co π.

Miejscami zerowymi funkcji kotangens są liczby postaci $x = \frac{π}{2} + k π$ , k∈Z

Znak funkcji kotangens w I i III ćwiartce jest dodatni, w II i IV ujemny.

Narysuj wykres funkcji kotangens