logowanie

Funkcja homograficzna

Funkcję wymierną postaci $f\left(x\right)=\frac{ax+b}{cx+d}$, gdzie ad ≠ bc, i c ≠ 0 nazywamy funkcją homograficzną.

Dziedziną funkcji homograficznej jest zbiór $x\in R\backslash \left\{-\frac{d}{c}\right\}$,
zbiorem wartości jest zbiór $y\in R\backslash \left\{\frac{a}{c}\right\}$,

Wykresem funkcji homograficznej $f\left(x\right)=\frac{ax+b}{cx+d}$ jest hiperbola mająca asymptotę pionową daną równaniem $x=-\frac{d}{c}$, oraz asymptotę poziomą daną równaniem $y=\frac{a}{c}$.
Jeżeli a ≠ 0 to miejscem zerowym funkcji homograficznej jest punkt $x=-\frac{b}{a}$.

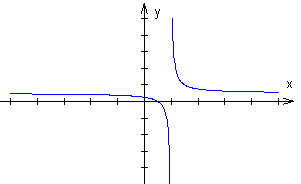
Wykres funkcji, gdy c ≠ 0 i ad - bc < 0


Wykres funkcji, gdy c ≠ 0 i ad - bc > 0

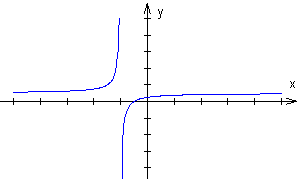
Funkcja $f\left(x\right)=\frac{ax+b}{cx+d}$ dla c ≠ 0 i ad - bc > 0 jest rosnąca w swojej dziedzinie, dla c ≠ 0 i ad - bc < 0 jest malejąca w swojej dziedzinie.

Funkcja homograficzna jest funkcją różnowartościową i ciągłą w swojej dziedzinie.
Gdy a = 0 i d = 0, wówczas funkcja homograficzna jest funkcją nieparzystą, a jej asymptotami są osie układu współrzędnych.

© 2023 math.edu.pl      kontakt