Funkcja kwadratowa
Jeżeli $a \neq 0$, to funkcję $f$ określoną wzorem $f(x) = ax^2 + bx + c$ nazywamy funkcją kwadratową.
$a, b, c$ - współczynniki liczbowe funkcji kwadratowej,
$\Delta = b^2 - 4ac$ - wyróżnik funkcji kwadratowej.
Dziedziną funkcji kwadratowej jest cały zbiór liczb rzeczywistych.
Zbiorem wartości funkcji dla $a \gt 0$ jest przedział $y \in [\frac{-\Delta}{4a}, +\infty)$,
dla $a \lt 0$ przedział $y \in (-\infty , \frac{-\Delta}{4a}]$.
Funkcję kwadratową można zapisać w postaci ogólnej, kanonicznej lub iloczynowej.
- postać ogólna: $f(x) = ax^2 + bx + c$
- postać kanoniczna: $f(x) = a(x - p)^2 + q$, gdzie $p = -\frac{b}{2a}, q = -\frac{\Delta}{4a}$
- postać iloczynowa: $f(x) = a(x - x_1)(x - x_2)$, gdzie $x_1, x_2$ są miejscami zerowymi funkcji.
Wykres funkcji kwadratowej
Wykresem funkcji kwadratowej jest parabola, o wierzchołku $W = (\frac{- b}{2a}, \frac{- \Delta}{4a})$, która jest obrazem paraboli
o równaniu $f(x) = ax^2$, w przesunięciu o wektor $\vec{u} = [\frac{- b}{2a}, \frac{- \Delta}{4a}]$.
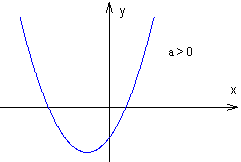
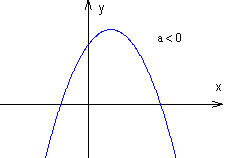
Gdy $a \gt 0$, to ramiona paraboli są skierowane w górę i posiada ona minimum globalne, w przeciwnym przypadku skierowane są w dół i
ma ona maksimum globalne. Miejscem przecięcia wykresu funkcji kwadratowej z osią $OY$ jest punkt $(0, c)$.
Miejsca zerowe funkcji kwadratowej
Liczba miejsc zerowych funkcji kwadratowej zależy od wartości wyróżnika $\Delta = b^2 - 4ac$.
Funkcja kwadratowa:
- posiada dwa miejsca zerowe dla $\Delta \gt 0$
$x_1 = \frac{-b - \sqrt{\Delta}}{2a}, x_2 = \frac{-b + \sqrt{\Delta}}{2a}$
- posiada jedno podwójne miejsce zerowe dla $\Delta = 0$
$x_1 = \frac{- b}{2a}$
- nie posiada miejsc zerowych dla $\Delta \lt 0$
Monotoniczność funkcji kwadratowej
Funkcja kwadratowa w pewnym przedziale jest funkcją rosnącą, a w pewnym malejącą.
Jeśli $a \gt 0$ funkcja jest:
- rosnąca dla $x \in (\frac{-b}{2a}, +\infty)$
- malejąca dla $x \in (-\infty, \frac{-b}{2a})$
Jeżeli $a \lt 0$ funkcja jest:
- rosnąca dla $x \in (-\infty , \frac{-b}{2a})$
- malejąca dla $x \in (\frac{-b}{2a}, +\infty)$