Funkcja logarytmiczna
Funkcja wykładnicza f(x) = ax dla a > 0 , a ≠ 1 jest funkcją ściśle monotoniczną, a więc różnowartościową, posiada zatem funkcję odwrotną. Funkcją odwrotną do funkcji wykładniczej nazywamy funkcją logarytmiczną i oznaczamy f(x) = logax.
Funkcję określoną wzorem f(x) = logax, gdzie x ∈ R+ i a ∈ R+\{1} nazywamy funkcją logarytmiczną o podstawie a.
Wykres i własności funkcji logarytmicznej
Monotoniczność funkcji logarytmicznej
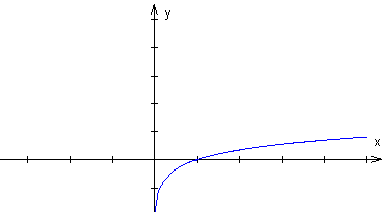
Jeżeli a > 1, to funkcja logarytmiczna
y = logax jest rosnąca w całej swojej
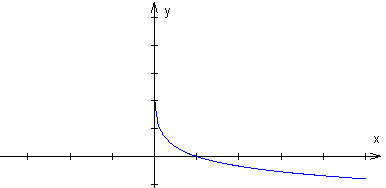
dziedzinie, a jeżeli a ∈ (0; 1), to funkcja logarytmiczna jest
malejąca.
a > 1
a ∈ (0; 1)
Wykresem funkcji logarytmicznej nazywamy krzywą logarytmiczną.
Dziedziną funkcji jest zbiór liczb rzeczywistych dodatnich,
Zbiorem wartości funkcji jest zbiór liczb rzeczywistych.
Inne własności
- funkcja logarytmicza jest różnowartościowa,
- funkcja logarytmicza jest wypukła,
- funkcja logarytmicza f(x) = logax
jest funkcją ciągłą spełniającą warunek
f(x1 ·
x2) = f(x1) +
f(x2) dla
x1, x2 ∈ R+.