Prosta, półprosta
Wśród linii wyróżniamy proste, łamane i krzywe. Linia prosta to pojęcie dla każdego zrozumiałe. Linia, która nie jest prostą, ale składa się z prostych części, nazywa się łamaną każda zaś linia, która nie jest prostą i nie składa się z części prostych, nazywa się krzywą.
O prostej możemy powiedzieć, że składa się z nieskończenie wielu punktów. Prostą oznaczamy małymi literami, najczęściej k, l, m, ...
Każda prosta, ma pewne własności, które odróżniają ją od innych linii.
Od jednego punktu do jakiegokolwiek drugiego, może prowadzić wiele dróg, ale
prosta jest tylko jedna. Tę własność prostej można sformułować w następujący
sposób:
Przez dwa różne punkty przechodzi dokładnie jedna prosta.
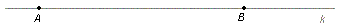
Jeśli dwie proste mają dwa różne punkty wspólne, to proste takie pokrywają się, czyli są równe. Stąd wniosek, że dwie różne proste mogą mieć co najwyżej jeden punkt wspólny.
Proste równoległe i proste prostopadłe
Jeśli proste na płaszczyźnie nie mają punktów wspólnych, to nazywamy je
równoległymi. Proste pokrywające się uznajemy również za równoległe.
Proste równoległe oznaczamy symbolem ||.
Dwie różne proste nazywamy prostopadłymi, jeżeli jedna z nich jest osią symetrii drugiej lub jeśli przecinają się pod kątem prostym. Proste prostopadłe oznaczamy symbolem ⊥.
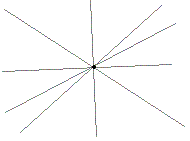
Mając dowolny punkt na płaszczyźnie, możemy przez niego poprowadzić dowolną ilość
prostych, które tworzą tak zwany pęk prostych. Punkt, przez który
przechodzą wszystkie proste, nazywa się wierzchołkiem pęku.
Jeśli na prostej obierzemy dowolny punkt A, to punkt ten dzieli tą prostą na dwie części. Każda z tych części zawierać będzie nieskończoną ilość punktów i każda z nich nazywa się półprostą. Punkt A nazywamy początkiem półprostej.

Odległość punktu od prostej
Odległość punktu A od prostej k jest równa odległości punktu
A od jego rzutu prostokątnego na prostą k.