Ostrosłup

Ostrosłupem nazywamy wielościan, którego jedna ściana, zwana podstawą ostrosłupa, jest dowolnym wielokątem, a pozostałe ściany, nazywane ścianami bocznymi ostrosłupa, są trójkątami o wspólnym wierzchołku.

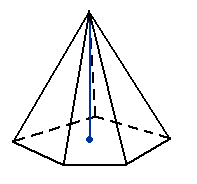
Wspólny wierzchołek ścian bocznych ostrosłupa nazywamy wierzchołkiem ostrosłupa.
Rzut prostokątny wierzchołka ostrosłupa na płaszczyznę podstawy nazywamy spodkiem wysokości ostrosłupa.
Wysokością ostrosłupa nazywamy odcinek łączący wierzchołek ostrosłupa ze spodkiem wysokości ostrosłupa.

Ostrosłup, którego podstawa jest n-kątem nazywamy ostrosłupem n-kątnym.

Sumę wszystkich ścian bocznych ostrosłupa nazywamy powierzchnią boczną graniastosłupa. Sumę powierzchni bocznej i podstawy ostrosłupa nazywamy powierzchnią całkowitą ostrosłupa.

Pole powierzchni całkowitej ostrosłupa o polu podstawy P_p i polu powierzchni bocznej P_b jest równe:
P_c = P_b + P_p

Objętość ostrosłupa o polu podstawy P_p i wysokości h jest równa
$V = \frac{1}{3} P_{p} \cdot H$

Przekrojem ostrosłupa nazywamy część wspólną ostrosłupa i płaszczyzny (przekrój poprzeczny - płaszczyzna przecina wszystkie krawędzie boczne, przekrój przekątny - płaszczyzna przechodzi przez dwie krawędzie nie należące do jednej ściany).

Ostrosłup nazywamy ostrosłupem prawidłowym, gdy jego podstawą jest wielokąt foremny i spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie.

Jeżeli ostrosłup jest prawidłowy, to wszystkie jego krawędzie boczne są równe, wszystkie kąty nachylenia krawędzi bocznych do płaszczyzny podstawy mają równe miary, wszystkie ściany boczne są przystającymi trójkątami równoramiennymi.

Czworościan foremny

Czworościanem foremnym nazywamy ostrosłup prawidłowy trójkątny, którego wszystkie ściany są trójkątami równobocznymi.

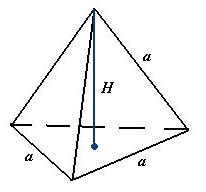
H - wysokość czworościanu,
a - krawędź czworościanu

$P_{c} = a^{2} \sqrt{3}$
$V = \frac{a^{2} \sqrt{3}}{12} \cdot H$

Ostrosłup ścięty

Ostrosłupem ściętym nazywamy część ostrosłupa zawartą między jego podstawą i przekrojem płaszczyzną równoległą do podstawy wraz z tą płaszczyzną.

Ściany boczne ostrosłupa ściętego są trapezami.
Podstawy ostrosłupa ściętego są wielokątami podobnymi.