Wzory matematyczne

Algebra
Potęga o wykładniku całkowitym ujemnym
Potęga o wykładniku wymiernym
Działania na potęgach
Działania na pierwiastkach
Wzory skróconego mnożenia
Prawa działań na logarytmach

Trygonometria
Związki pomiędzy funkcjami
Funkcje kąta podwójnego
Funkcje połowy kąta
Funkcje sumy i różnicy kątów
Wzory redukcyjne

Analiza matematyczna
Pochodne funkcji elementarnych

Kombinatoryka
Silnia
Symbol Newtona
Permutacje
Permutacje z powtórzeniami
Wariacje bez powtórzeń
Wariacje z powtórzeniami
Kombinacje
Kombinacje z powtórzeniami

Geometria
Trójkąt
Twierdzenie sinusów, kosinusów
Twierdzenie Pitagorasa
Czworokąty
Koło i okrąg

Graniastosłupy
Ostrosłupy
Bryły obrotowe

Potęga o wykładniku całkowitym ujemnym
a^-n = $\frac{1}{a^{n}}$ dla a ∈ R\{0} ∧ n ∈ N

Potęga o wykładniku wymiernym
$a^{\frac{m}{n}} = \sqrt[n]{a^{m}}$ dla a ∈ R⁺∪{0}, m ∈ N i n ∈ N\{1}
$a^{- \frac{m}{n}} = \frac{1}{\sqrt[n]{a^{m}}}$ dla a ∈ R⁺, m ∈ N i n ∈ N\{1}

Działania na potęgach
Jeżeli m, n ∈ R i a, b ∈ R⁺ albo m, n ∈ Z i a, b ∈ R i a ≠ 0 i b ≠ 0, to:
a^m · aⁿ = a^m+n
$\frac{a^{m}}{a^{n}}$ = a^m-n
(a · b)^m = a^m · b^m
${(\frac{a}{b})}^{m} = \frac{a^{m}}{b^{m}}$
(a^m)ⁿ = a^m·n

Działania na pierwiastkach
Jeżeli a ≥ 0, b ≥ 0, n ∈ N\{0, 1}, to:
$\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}$
$\sqrt[m]{\sqrt[n]{a}} = \sqrt[m n]{a}$
${(\sqrt[n]{a})}^{m} = \sqrt[n]{a^{m}}$
$a \cdot \sqrt[n]{b} = \sqrt[n]{a^{n} b}$
${(\sqrt[n]{a})}^{n} = a$
$\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ dla b > 0

Wzory skróconego mnożenia
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
a² - b² = (a - b)(a + b)
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a - b)³ = a³ - 3a²b + 3ab² - b³
a³ + b³ = (a + b)(a² - ab + b²)
a³ - b³ = (a - b)(a² + ab + b²)

Prawa działań na logarytmach
Przy założeniu: a > 0, a ≠ 1, b > 0, b ≠ 1, x > 0, y > 0:
log_a(x · y) = log_ax + log_ay
${log}_{a} \frac{x}{y} = {log}_{a} x - {log}_{a} y$
${log}_{a} x^{y} = y {log}_{a} x$
${log}_{a} \sqrt[n]{x} = \frac{1}{n} {log}_{a} x$
${log}_{b} x = \frac{{log}_{a} x}{{log}_{a} b}$
${log}_{a} b = \frac{1}{{log}_{b} a}$

Związki pomiędzy funkcjami trygonometrycznymi
$tg x = \frac{sin x}{cos x} = \frac{1}{ctg x}$
$ctg x = \frac{cos x}{sin x} = \frac{1}{tg x}$
sin²x + cos²x = 1 (jedynka trygonometryczna)
tgα · ctgα = 1

Funkcje kąta podwójnego
sin2α = 2sinαcosα
cos2α = cos²α - sin²α = 2cos²α - 1
tg2α = $\frac{2 tg α}{1 - {tg}^{2} α}$
ctg2α = $\frac{{ctg}^{2} α - 1}{2 ctg α}$

Funkcje połowy kąta
$sin \frac{α}{2} = ą \sqrt{\frac{1 - cos α}{2}}$
$cos \frac{α}{2} = ą \sqrt{\frac{1 + cos α}{2}}$
$tg \frac{α}{2} = \frac{1 - cos α}{sin α}$
$ctg \frac{α}{2} = \frac{1 + cos α}{sin α}$

Funkcje sumy i różnicy kątów
sin(α + β) = sinαcosβ + cosαsinβ
cos(α + β) = cosαcosβ - sinαsinβ
sin(α - β) = sinαcosβ - cosαsinβ
cos(α - β) = cosαcosβ + sinαsinβ

tg(α + β) = $\frac{tg α + tg β}{1 - tg α \cdot tg β}$
ctg(α + β) = $\frac{ctg α \cdot ctg β - 1}{ctg α + ctg β}$
tg(α - β) = $\frac{tg α - tg β}{1 + tg α \cdot tg β}$
ctg(α - β) = $\frac{ctg α \cdot ctg β + 1}{ctg α - ctg β}$

Wzory redukcyjne
sin(90° + α) = cosα cos(90° + α) = -sinα tg(90° + α) = -ctgα ctg(90° + α) = -tgα sin(270° + α) = -cosα cos(270° + α) = sinα tg(270° + α) = -ctgα ctg(270° + α) = -tgα	sin(180° + α) = -sinα cos(180° + α) = -cosα tg(180° + α) = tgα ctg(180° + α) = ctgα sin(360° + α) = sinα cos(360° + α) = cosα tg(360° + α) = tgα ctg(360° + α) = ctgα

Silnia n! = 1 · 2 · 3 · ... · n

Symbol Newtona Dla n, k∈N i 0 ≤ k ≤ n $(\begin{matrix} n \\ k \end{matrix}) = \frac{n!}{k! (n - k)!}$

Permutacje P_n = n!

Permutacje z powtórzeniami $P_{n}^{n_{1}, n_{2}, ..., n_{k}} = \frac{n!}{n_{1}! n_{2}! ... n_{k}!}$

Wariacje bez powtórzeń $V_{n}^{k} = \frac{n!}{(n - k)!}$

Wariacje z powtórzeniami $W_{n}^{k} = n^{k}$

Kombinacje $C_{n}^{k} = (\begin{matrix} n \\ k \end{matrix}) = \frac{n!}{k! \cdot (n - k)!}$

Kombinacje z powtórzeniami ${\bar{C}}_{n}^{k} = (\begin{matrix} n + k - 1 \\ k \end{matrix}) = \frac{(n + k - 1)!}{k! \cdot (n - 1)!}$

Pochodne funkcji elementarnych

Funkcja	Pochodna funkcji	Uwagi

y = c	y' = 0	c∈R
y = x^α	y' = αx^α-1	α∈R (x zależne od α)
y = $\frac{1}{x}$	y' = $- \frac{1}{x^{2}}$	x∈R\{0}
y = $\sqrt{x}$	y' = $\frac{1}{2 \sqrt{x}}$	x∈R⁺∪{0}
y = a^x	y' = a^xlna	x∈R, a∈R⁺
y = e^x	y' = e^x	x∈R
y = log_ax	y' = $\frac{1}{x}$ log_ae = $\frac{1}{x ln a}$	x∈R⁺, a∈R⁺\{1}
y = lnx	y' = $\frac{1}{x}$	x∈R⁺
y = sinx	y' = cosx	x∈R
y = cosx	y' = -sinx	x∈R
y = tgx	y' = $\frac{1}{{cos}^{2} x}$	x∈R, x≠ $\frac{1}{2}$ π + kπ, k∈C
y = ctgx	y' = $- \frac{1}{{sin}^{2} x}$	x∈R, x≠kπ, k∈C
y = arcsinx	y' = $\frac{1}{\sqrt{1 - x^{2}}}$	x∈(-1, 1)
y = arccosx	y' = $- \frac{1}{\sqrt{1 - x^{2}}}$	x∈(-1, 1)
y = arctgx	y' = $\frac{1}{1 + x^{2}}$	x∈R
y = arcctgx	y' = $- \frac{1}{1 + x^{2}}$	x∈R

Trójkąt

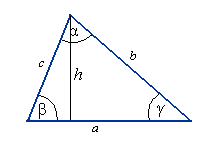
Ob = a + b + c

$P = \frac{1}{2} a h$

$P = \frac{1}{2} a b sin γ = \frac{1}{2} b c sin α = \frac{1}{2} a c sin β$ ,

$P = \sqrt{p (p - a) (p - b) (p - c)}$ ,    gdzie $p = \frac{1}{2} (a + b + c)$ , (wzór Herona)

$R = \frac{a b c}{4 P}$ ,     (promień okręgu opisanego),

$r = \frac{P}{p}$ ,     (promień okręgu wpisanego).

Twierdzenie sinusów, kosinusów

      $\frac{a}{sin α} = \frac{b}{sin β} = \frac{c}{sin γ} = 2 r$

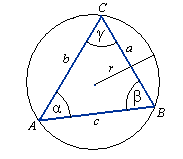
      c² = a² + b² - 2abcosγ
      b² = a² + c² - 2accosβ
      a² = b² + c² - 2bccosα

Twierdzenie Pitagorasa
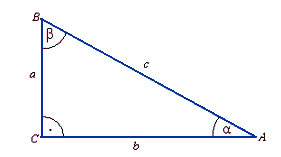
trójkąt prostokątny

a² + b² = c²

Czworokąty

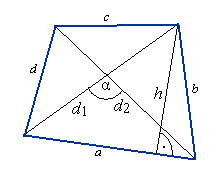
Ob = a + b + c + d
$P = \frac{1}{2} d_{1} \cdot d_{2} \cdot sin α$
d₁, d₂ - przekątne czworokąta,
α - kąt zawarty między przekątnymi
h - wysokość czworokąta

Pole czworokąta wpisanego w okrąg:
$P = \sqrt{(p - a) (p - b) (p - c) (p - d)}$ ,    gdzie $p = \frac{1}{2} (a + b + c + d)$

Trapez
trapez
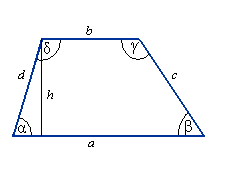
Obwód trapezu:     Ob = a + b + c + d
Pole trapezu:     $P = \frac{1}{2} (a + b) \cdot h$

Równoległobok

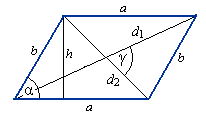
Ob = 2a + 2b
P = a · h = a · b · sinα
$P = \frac{1}{2} d_{1} \cdot d_{2} \cdot sin γ$

Romb
romb
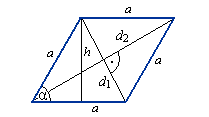
Ob = 4a
P = a · h = a² · sinα
$P = \frac{1}{2} d_{1} \cdot d_{2}$

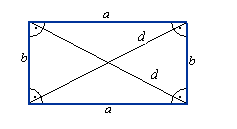
Prostokąt

Ob = 2a + 2b
P = a · b
$d = \sqrt{a^{2} + b^{2}}$

Kwadrat
kwadrat
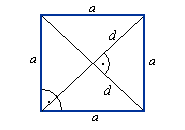
Ob = 4a
P = a²
$P = \frac{1}{2} d^{2}$
$d = a \sqrt{2}$

Deltoid
deltoid
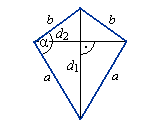
Ob = 2a + 2b
$P = \frac{1}{2} d_{1} \cdot d_{2}$
P = a · b · sinα

Koło i okrąg
koło
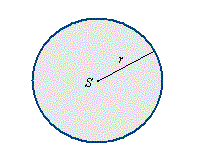
r - promień koła,     π = 3,1415...

Pole koła     P = πr²
Długość okręgu     L = 2πr
Długość łuku     $l = \frac{α}{360 °} \cdot 2 π r$

Pole wycinka koła o kącie środkowym α     $P = \frac{α}{360 °} π r^{2}$
Pole odcinka koła o kącie środkowym α     $P = \frac{α}{360 °} π r^{2} - \frac{r^{2} sin α}{2}$

Graniastosłupy

Pole powierzchni całkowitej: P_c = P_b + 2P_p
Objętość graniastosłupa: V = P_p · H

Sześcian

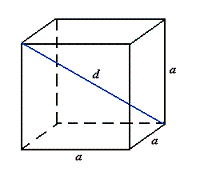
P_c = 6a²

V = a³

$d = a \sqrt{3}$

Długość promienia kuli wpisanej
$r = \frac{1}{2} a$
Długość promienia kuli opisanej
$R = \frac{1}{2} d = \frac{a \sqrt{3}}{2}$

Prostopadłościan

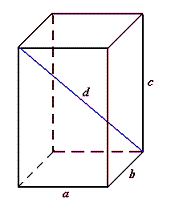
P_c = 2ab + 2bc + 2ac

V = abc

$d = \sqrt{a^{2} + b^{2} + c^{2}}$

Ostrosłupy

Pole powierzchni całkowitej: P_c = P_b + P_p
Objętość ostrosłupa: $V = \frac{1}{3} P_{p} \cdot H$

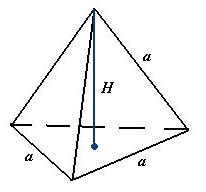
Czworościan foremny

czworościan foremny

$P_{c} = a^{2} \sqrt{3}$
$V = \frac{a^{3} \sqrt{2}}{12}$

Bryły obrotowe

Walec

walec
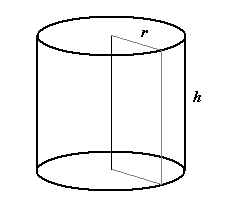
Pole powierzchni bocznej: P_b = 2πrh

Pole powierzchni całkowitej: P_c = 2πr(r + h)

Objętość: V = πr²h

Stożek

stożek
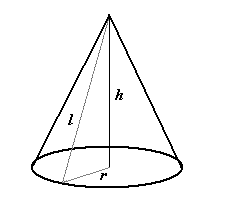
Pole powierzchni bocznej: $P_{b} = π r l$

Pole powierzchni całkowitej: $P_{c} = π r (r + l)$

Objętość: $V = \frac{1}{3} π r^{2} h$

Kula

kula
Pole powierzchni całkowitej: $P = 4 π r^{2}$

Objętość: $V = \frac{4}{3} π r^{3}$