logowanie

Okrąg i koło

Koło znane było we wszystkich kulturach od najdawniejszych czasów. Zastosowane zostało tam, gdzie zachodziła potrzeba transportu na większe odległości. Wykorzystanie koła jako koło jezdne pojawiło się ok. 3500 lat p.n.e. w Mezopotamii. Trudno sobie wyobrazić świat bez koła, tę figurę rozpoznaje każdy. Z pojęciem koła wiąże się pojęcie okręgu, które można określić jako krzywą, którą zakreśla koniec odcinka, obracającego się dokoła pewnego danego punktu.

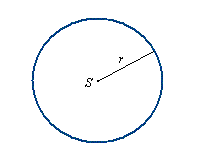
Okręgiem nazywamy krzywą, której wszystkie punkty leżą w tej samej odległości od danego punktu zwanego środkiem okręgu.
     r - promień okręgu
     S - środek okręgu

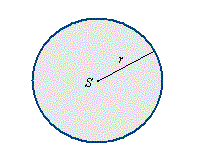
Koło to część płaszczyzny ograniczona okręgiem wraz z tym okręgiem.
     r - promień koła
     S - środek koła

Odcinek, który łączy dowolny punkt okręgu ze środkiem okręgu (koła), to promień okręgu (koła).
Okrąg o środku S i promieniu długości r oznaczamy o(S, r).
Koło o środku S i promieniu długości r oznaczamy k(S, r).

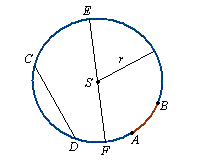
Łuk okręgu to jedna z dwóch części okręgu wyznaczona przez dwa punkty tego okręgu (AB).
Cięciwa okręgu (koła) to odcinek łączący dwa różne punkty okręgu (CD).
Średnica okręgu (koła) - to najdłuższa z jego cięciw, która przechodzi przez środek okręgu (koła) (EF).

Pole koła (P) i długość okręgu (L):
P = πr²
L = 2πr

gdzie π (pi) to stosunek długości okręgu do długości jego średnicy, który jest wielkością stałą i wynosi w przybliżeniu 3,1415..., a r to długość promienia koła.

Sieczna to prosta mająca z okręgiem dokładnie dwa punkty wspólne, prostą mająca dokładnie jeden punkt wspólny nazywamy styczną do okręgu.

Kąt wpisany i kąt środkowy
Wycinek koła, odcinek koła

© 2024 math.edu.pl      kontakt