Przedzia³y liczbowe
W zbiorze liczb rzeczywistych wyró¿niamy podzbiory zwane przedzia³ami liczbowymi. Przedzia³y liczbowe dzielimy na przedzia³y ograniczone i nieograniczone (nieskoñczone).
Dla danych liczb $a$ i $b$ takich, ¿e $a \lt b$ definiuje siê przedzia³y liczbowe nastêpuj±co:
Przedzia³y ograniczone:
$(a; b) = \{x: a \lt x \lt b\}$ - przedzia³ obustronnie otwarty
$[a; b] = \{x: a \le x \le b\}$ - przedzia³ obustronnie domkniêty
$[a; b) = \{x: a \le x \lt b\}$ - przedzia³ lewostronnie domkniêty
$(a; b] = \{x: a \lt x \le b\}$ - przedzia³ prawostronnie domkniêty
Przedzia³y nieograniczone:
$(-\infty; a) = \{x: x \lt a\}$ - przedzia³ prawostronnie otwarty
$(-\infty; a] = \{x: x \le a\}$ - przedzia³ prawostronnie domkniêty
$(a; +\infty) = \{x: a ≥ x\}$ - przedzia³ lewostronnie otwarty
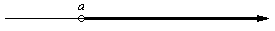
$[ a; +\infty) = \{x: a \gt x\}$ - przedzia³ lewostronnie domkniêty
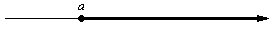
$(-\infty; +\infty) = R$ - ca³a o¶ liczbowa.