Twierdzenie Ptolemeusza
Twierdzenie Ptolemeusza – opisuje czworokąt wpisany w okrąg. Jego sformułowanie oraz dowód przypisuje się Klaudiuszowi Ptolemeuszowi, wybitnemu astronomowi i matematykowi.
W dowolnym czworokącie ABCD wpisanym w okrąg iloczyn długości przekątnych równy jest sumie iloczynów
długości przeciwległych boków.
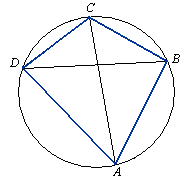
|AC| · |BD| = |AB| · |CD| + |BC| · |AD|.
Dla czworokątów, które nie dają się wpisać w okrąg, iloczyn długości przekątnych jest mniejszy od sumy
iloczynów długości boków przeciwległych. Jest to tzw. nierówność Ptolemeusza.
|AC| · |BD| < |AB| · |CD| + |BC| · |AD|.