Wielokąt
Wielokątem nazywamy figurę płaską będącą sumą łamanej zwyczajnej zamkniętej i obszaru ograniczonego wyciętego z płaszczyzny przez tę łamaną. Wielokąt o n bokach nazywamy również n-kątem. Najczęściej spotykanymi wielokątami są trójkąty i czworokąty.
Wielokątem (wielobokiem) nazywamy część płaszczyzny ograniczoną łamaną zwyczajną zamkniętą wraz z tą łamaną.
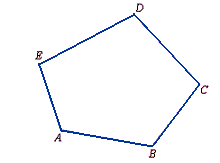
Odcinki, tworzące wielokąt, nazywamy jego bokami, a punkty ich przecięcia wierzchołkami wielokąta. Sumę wszystkich boków nazywamy obwodem wielokąta. Linię łamaną ABCDEA ograniczającą wielokąt nazywamy brzegiem wielokąta. Brzeg wielokąta dzieli płaszczyznę na dwa obszary, z których jeden jest ograniczony, nazywamy go wewnętrznym, drugi jest nieograniczony i nazywamy go obszarem zewnętrznym.
Przekątną wielokąta nazywamy odcinek, który łączy dwa niekolejne wierzchołki wielokąta. Liczba przekątnych n-kąta jest równa
Wielokąty wklęsłe i wypukłe
Jeżeli wszystkie kąty wewnętrzne wielokąta są kątami wypukłymi, to wielokąt ten nazywamy
wielokątem wypukłym.
Jeżeli co najmniej jeden kąt wewnętrzny wielokąta jest kątem wklęsłym, to wielokąt ten nazywamy
wielokątem wklęsłym.
Kąty wewnętrzne i zewnętrzne wielokąta
Kąty utworzone przez dowolne dwa kolejne boki nazywamy kątami wewnętrznymi wielokąta.
Kąt zewnętrzny wielokąta - to kąt przyległy do kąta wewnętrznego tego wielokąta.
Suma miar kątów wewnętrznych n-kąta jest równa (n - 2) · 180°.
Suma miar kątów zewnętrznych każdego wielokąta wypukłego jest równa 360°.
Wielokąty przystające
W dwóch wielokątach przystających takie dwa punkty, takie dwa odcinki oraz takie dwa kąty nazywamy
odpowiednimi, które po nałożeniu jednego wielokąta na drugi, pokrywają się. W wielokątach przystających
odpowiednie boki mają równe długości i odpowiednie kąty mają równe miary.
Wielokąt wpisany i opisany na okręgu
Wielokąt, którego wszystkie wierzchołki należą do pewnego okręgu, nazywamy wielokątem wpisanym
w okrąg, a okrąg ten nazywamy okręgiem opisanym na wielokącie.
Na wielokącie można opisać okrąg wtedy i tylko wtedy, gdy symetralne wszystkich boków wielokąta
przecinają się w jednym punkcie. Punkt ten jest środkiem okręgu opisanego na wielokącie.
Wielokąt, którego wszystkie boki są styczne do pewnego okręgu, nazywamy wielokątem opisanym na okręgu,
a okrąg ten nazywamy okręgiem wpisanym w wielokąt.
W wielokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy dwusieczne wszystkich kątów wielokąta
przecinają się w jednym punkcie. Punkt ten jest środkiem okręgu wpisanego w wielokąt.
Pole wielokąta o obwodzie l opisanego na okręgu o promieniu r równe jest
.