Trójkąty

Wielokąt o najmniejszej liczbie boków to trójkąt.

Trójkąt to płaszczyzna ograniczona łamaną zwyczajną zamkniętą złożoną z trzech odcinków.

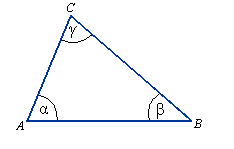
punkty A, B, C to wierzchołki trójkąta,
odcinki AB, BC, CA to boki trójkąta,
kąty α, β, γ to kąty wewnętrzne trójkąta.

Często jeden z boków nazywamy jego podstawą, a dwa pozostałe ramionami trójkąta.

Wysokością trójkąta nazywamy najkrótszy odcinek łączący wierzchołek trójkąta z przeciwległym bokiem (lub jego przedłużeniem). Jest on zawsze prostopadły do tego boku.
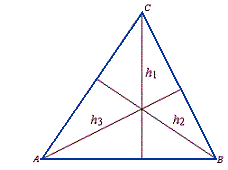
wysokość trójkąta

Każdy trójkąt ma trzy wysokości, które przecinają się w jednym punkcie zwanym ortocentrum.

Kątem zewnętrznym trójkąta nazywamy kąt przyległy do kąta wewnętrznego. Miara kąta zewnętrznego trójkąta jest równa sumie miar dwóch kątów wewnętrznych do niego nieprzyległych.

Dwusieczna kąta wewnętrznego trójkąta dzieli bok przeciwległy na dwa odcinki, których stosunek długości jes równy stosunkowi długości pozostałych boków. Każdy trójkąt ma trzy dwusieczne przecinające się w jednym punkcie, który jest środkiem koła wpisanego w trójkąt.

Symetralną boku trójkąta nazywamy prostą prostopadłą do tego boku i przechodzącą przez jego środek. Każdy trójkąt ma trzy symetralne boków, przecinające się w jednym punkcie, który jest środkiem koła opisanego na tym trójkącie.

Środkowe trójkąta przecinają się w punkcie, który nazywamy środkiem ciężkości trójkąta. Punkt ten dzieli każdą ze środkowych na dwie części, z których odcinek łączący wierzchołek z punktem jest dwa razy dłuższy od pozostałej części tej środkowej.

P - pole trójkąta,
Ob - obwód trójkąta,

Dla dowolnego trójkąta zachodzi:

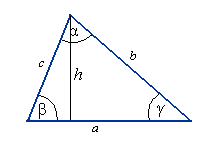
|a - b| < c < a + b,
α + β + δ = 180°,
Ob = a + b + c,
$P = \frac{1}{2} a h$

$P = \frac{1}{2} a b sin γ = \frac{1}{2} b c sin α = \frac{1}{2} a c sin β$ ,

$P = \sqrt{p (p - a) (p - b) (p - c)}$ ,     gdzie $p = \frac{1}{2} (a + b + c)$ , (wzór Herona)

$R = \frac{a b c}{4 P}$ ,     (promień okręgu opisanego),

$r = \frac{P}{p}$ ,     (promień okręgu wpisanego).

Podział trójkątów ze względu na boki
trójkąt różnoboczny
trójkąt równoramienny
trójkąt równoboczny

Podział trójkątów ze względu na kąty
trójkąt ostrokątny
trójkąt prostokątny
trójkąt rozwartokątny

Klasyfikacja trójkątów
Cechy podobieństwa trójkątów
Cechy przystawania trójkątów
Twierdzenie sinusów i twierdzenie kosinusów