Wielościany foremne

Wielościanem foremnym nazywamy wielościan wypukły, którego wszystkie ściany są przystającymi wielokątami foremnymi i wszystkie kąty dwuścienne wyznaczone przez ściany są równe.

Istnieją tylko następujące wielościany foremne:

Czworościan (tetraedr)
4 ściany trójkątne, 4 wierzchołki, 6 krawędzi.

P = \sqrt{3} a^{2}

V = \frac{\sqrt{2}}{12} a^{3}

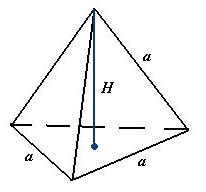
Sześcian (heksaedr)
6 ścian kwadratowych, 8 wierzchołków, 12 krawędzi.

$P = 6 a^{2}$
$V = a^{3}$

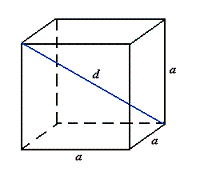
Ośmiościan (oktaedr)
8 ścian trójkątnych, 6 wierzchołków, 12 krawędzi.

$P = 2 \sqrt{3} a^{2}$
$V = \frac{\sqrt{2}}{3} a^{3}$

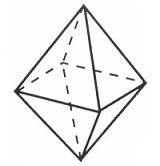
Dwunastościan (dodekaedr)
12 ścian pięciokątnych, 20 wierzchołków, 30 krawędzi.

$P = 15 (\sqrt{5} + 2) a^{2}$
$V = \frac{(15 + 7 \sqrt{5})}{4} a^{3}$

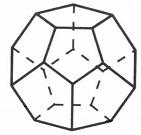
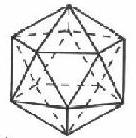
Dwudziestościan (ikosaedr)
20 ścian trójkątnych, 12 wierzchołków, 30 krawędzi.

$P = 5 \sqrt{3} a^{2}$
$V = \frac{5 (3 + \sqrt{5})}{12} a^{3}$

Dlaczego wielościanów foremnych nie może być więcej niż pięć?
Suma wszystkich kątów płaskich kąta bryłowego musi być mniejsza od 360°. Z trójkątów można zbudować trzy wielościany foremne, gdzie z jednego wierzchołka mogą wychodzić:
- 3 krawędzie (60° × 3 = 180° < 360°)
- 4 krawędzie (60° × 4 = 240° < 360°)
- 5 krawędzi (60° × 5 = 300° < 360°).
Z kwadratów składać się może tylko jeden wielościan (3 × 90° = 270°). Z pięciokątów foremnych składać się może również tylko jeden, gdyż kąt pięciokąta foremnego ma miarę 108° (3 × 108° < 360°). Z sześciokątów, ani tym bardziej z wielokątów o większej liczbie boków, wielościanu foremnego zbudować się nie da.

Wielościany foremne znali już Pitagorejczycy w VI w. p.n.e. i pod postaciami sześcianu, ośmiościanu, czworościanu i dwudziestościanu wyobrażali cztery żywioły: ziemię, powietrze, ogień i wodę, a od czasów Platona uważano piąty wielościan foremny, dwunastościan, za postać wszechświata. Wielościany te noszą nazwę brył platońskich