Cechy przystawania trójkątów

Cechy przystawania trójkątów, to warunki konieczne i wystarczające na to, aby dwa trójkąty były przystające, czyli takie same. Przystawanie figur geometrycznych oznaczamy symbolem ≡.

I cecha przystawania trójkątów

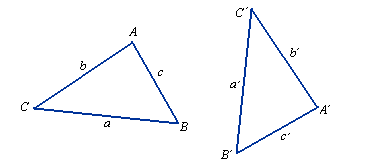
cechy podobieństwa trójkątów
a = a'
b = b'
c = c'
ΔABC ≡ ΔA'B'C'

Jeżeli trzy boki jednego trójkąta są odpowiednio równe trzem bokom drugiego trójkąta, to trójkąty są przystające.

II cecha przystawania trójkątów

cechy podobieństwa trójkątów
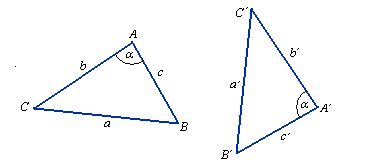
α = α'
b = b'
c = c'
ΔABC ≡ ΔA'B'C'

Jeżeli dwa boki i kąt między nimi zawarty jednego trójkąta są odpowiednio równe dwóm bokom i kątowi między nimi zawartemu drugiego trójkąta, to trójkąty są przystające.

III cecha przystawania trójkątów

cechy podobieństwa trójkątów
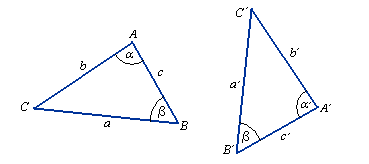
α = α'
c = c'
β = β'
ΔABC ≡ ΔA'B'C'

Jeżeli długość boku i dwa kąty do niego przyległe jednego trójkąta są odpowiednio równe długości boku i dwóm kątom do niego przyległym drugiego trójkąta, to trójkąty są przystające.