Czworokąt wpisany i opisany na okręgu

Czworokąt wpisany w okrąg

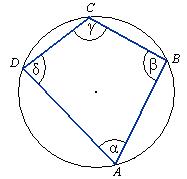
Jeżeli na danym okręgu obierzemy cztery dowolne punkty A, B, C i D i połączymy je kolejno, to otrzymamy czworokąt ABCD wpisany w okrąg. czworokąt wpisany

W czworokącie wpisanym w okrąg suma przeciwległych kątów wynosi 180°.
α + γ = 180°,
β + δ = 180°.

Pole czworokąta wpisanego w okrąg:
$P = \sqrt{(p - a) (p - b) (p - c) (p - d)}$ ,
gdzie $p = \frac{1}{2} (a + b + c + d)$

Dowolny czworokąt można wpisać w okrąg wtedy, gdy symetralne wszystkich jego boków przecinają się w jednym punkcie.
Czworokąt wypukły można wpisać w okrąg wtedy i tylko wtedy, gdy sumy miar kątów przeciwległych są równe i wynoszą 180°

Dowolny czworokąt wpisany w okrąg spełnia Twierdzenie Ptolemeusza.

Czworokąt opisany na okręgu

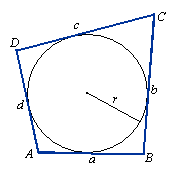
Jeżeli na okręgu obierzemy cztery punkty i poprowadzimy przez nie styczne, to punkty przecięcia kolejnych stycznych będą wierzchołkami czworokąta opisanego na okręgu. czworokąt opisany

W czworokącie opisanym na okręgu sumy długości przeciwległych boków tego czworokąta są równe.
a + c = b + d

Pole czworokąta opisanego na okręgu o promieniu r:
$P = \frac{1}{2} r (a + b + c + d)$

W dowolny czworokąt można opisać na okręgu tylko wtedy, gdy dwusieczne wszystkich jego kątów przecinają się jednym punkcie, który jest środkiem okręgu.
Czworokąt wypukły można opisać na okręgu wtedy i tylko wtedy, gdy sumy długości przeciwległych boków czworokąta są równe.