Kąt płaski
Jeżeli na płaszczyźnie z danego punktu poprowadzimy dwie półproste, to utworzymy figurę, która posłuży nam do określenia pojęcia kąta. Półproste wówczas nazywamy ramionami, a ich wspólny punkt wierzchołkiem kąta.
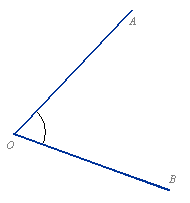Kąt płaski (kąt) to każda z dwóch części płaszczyzny ograniczonych dwiema półprostymi o wspólnym początku (
zwanym wierzchołkiem kąta) wraz z tymi półprostymi (zwanymi ramionami kąta).
Dla oznaczenia kątów używamy pojedynczych liter alfabetu greckiego: α, β, γ, δ, ... lub zapisujemy symbolicznie ∡AOB, gdzie środkowa litera oznacza wierzchołek kąta. Najczęściej, zamiast malowania płaszczyzny między ramionami rysujemy łuk wewnątrz kąta.
Kąt wypukły i kąt wklęsły
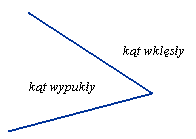
Jeśli założymy, że ramiona kąta nie leżą na jednej prostej, to tylko jeden z
kątów - nazwiemy go wewnętrznym - ma tę własność, że odcinek łączący dwa dowolne
punkty na różnych ramionach figury zawiera się w tym obszarze. Kąt o tej własności
nazywamy kątem wypukłym. Drugi z kątów, który nie posiada tej własności
nazywamy kątem wklęsłym.
Miara kąta wypukłego jest mniejsza lub równa π (180°) oraz równa 2π
(360°).
Miara kąta wklęsłego jest większa od π (180°) lecz mniejsza niż 2π
(360°).
Dwusieczna kąta
Dwusieczną kąta nazywamy półprostą, która dzieli dany kąt na dwa przystające kąty.
Dwusieczna kąta jest półprostą zawartą w jego osi symetrii, a każdy punkt
dwusiecznej kąta jest równo odległy od obu ramion kąta.
Jednostki miary kąta płaskiego
Rodzaje kątów
Kąty przyległe i wierzchołkowe
Kąty naprzemianległe i odpowiadające
Twierdzenie Talesa