Twierdzenie Pitagorasa
Pitagoras to postać związana szczególnie z rozwojem matematyki, gdy przyszedł na świat, Grecja już wiele umiała. Stawiano już wówczas wspaniałe budowle, które po dziś dzień są przedmiotem podziwu, a mieszkania wykładano parkietem. Grecy byli mistrzami w układaniu parkietów, a sztuka ich układania nie była obca Pitagorasowi, który zaczął się zastanawiać dlaczego niektóre trójkąty, których boki zachowuję pewne określone proporcje są zawsze prostokątne. W jakiej zależności pozostają ze sobą te trójkąty i co wspólnego w ogóle mają te trójkąty z kwadratami?
Pitagoras wyjechał do Egiptu, aby tam poznać tajemnice nauk, w których liczba grała główną rolę. Po powrocie w Krotonie założył szkołę pitagorejską, w której wprowadzał swoich uczniów w tajniki liczb. Dla pitagorejczyków liczba była podstawą wszechświata, wszystkie zjawiska tłumaczyli działaniem liczb. Pitagorejczycy eksperymentowali, szukali i badali wspólne cechy liczb, w ten sposób ta tajemnicza, prawie że religijna sekta matematyków odkryła liczby dotyczące trójkątów, kwadratów i pięciokątów. Pitagorejczycy pytali: jak znaleźć trójkąty prostokątne, których długości boków można wyrazić liczbami całkowitymi? Stosunkowo łatwo rozwiązali ten problem, właściwie rozwiązali nowoczesne równania kwadratowe: a2 + b2 = c2 i doszli do wniosku, że boki trójkąta tylko wówczas można wyrazić liczbami całkowitymi, kiedy a = 2x + 1, b = 2(x2 + x), c = 2x2 + 2x + 1, gdzie za x możemy podstawić dowolną liczbę całkowitą.
Najważniejszym osiągnięciem pitagorejczyków było sformułowanie twierdzenia, które otrzymało nazwę twierdzenia Pitagorasa, które umożliwiło człowiekowi zbliżenie się za pomocą matematyki do poznania gwiazd, i bez którego cała geometria jest nie do pomyślenia. Oto treść twierdzenia:
Kwadrat zbudowany na przeciwprostokątnej trójkąta prostokątnego jest równy sumie kwadratów zbudowanych na
przyprostokątnych tego trójkąta.
a2 + b2 = c2
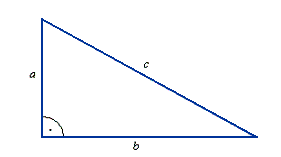
Grecy nadali bokom trójkąta osobne nazwy, które przetrwały do dziś. I tak o boku leżącym naprzeciw kąta
prostego mówimy jako o przeciwprostokątnej i oznaczamy ją literą c, a pozostałe dwa boki nazywamy
przyprostokątnymi i oznaczamy literami a oraz b. Twierdzenie Pitagorasa było czymś zupełnie
nowym w rozwoju ówczesnej matematyki, odnosiło się do wszystkich trójkątów i było słuszne zawsze i wszędzie.
Prawdziwość twierdzenia Pitagorasa udowodniła już jego szkoła, jednak nie zachowały się żadne dokumenty.
Znamy natomiast dowody Euklidesa, z których najczęściej przytacza się dowód równoważności pól.
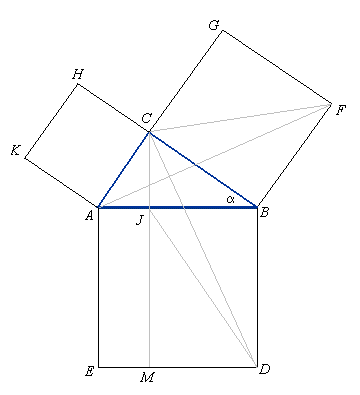
Niech będzie dany trójkąt prostokątny ABC i na jego bokach kwadraty BFGC, ACHK,
AEDB. Wierzchołek C połączmy z punktem D, a wierzchołek A z punktem F.
W kwadracie BFGC narysujmy przekątną CF. Trójkąt ABF jest równy trójkątowi BDC,
ponieważ długość boku AB równa jest długości boku BD oraz długość boku BF równa jest
długości boku BC. Kąt ABF równy jest kątowi 90° + α, czyli równy kątowi DBC.
Pole trójkąta DBC równe jest polu trójkąta DBJ, a pole trójkąta BFA równe jest polu
trójkąta BFC, więc trójkąty DBJ i BFC mają również równe pola. Dalej widzimy, że pole
trójkąta DBJ równe jest połowie pola prostokąta MDBJ, podobnie pole trójkąta BFC równe
jest połowie pola kwadratu BFGC. Jeżeli pola tych dwóch trójkątów są sobie równe, to muszą być równe
pola MDBJ i BFGC. Podobnie postępujemy z prostokątem EMJA, aby przekonać się, że jego
pole równe jest polu kwadratu ACHK. Ostatecznie otrzymamy, że AEDB = BFGC + ACHK,
co dowodzi prawdziwości twierdzenia Pitagorasa.
Twierdzenie Pitagorasa w innej postaci znali już starożytni Babilończycy, którzy około w 2000 lat przed naszą erą obliczali przeciwprostokątną trójkąta prostokątnego ze wzoru .
Twierdzenie odwrotne do twierdzenia Pitagorasa jest również prawdziwe i brzmi: jeżeli suma kwadratów długości dwóch boków trójkąta, jest równa kwadratowi długości trzeciego boku trójkąta, to trójkąt ten jest prostokątny.