Twierdzenie sinusów i kosinusów

Twierdzenie sinusów, twierdzenie kosinusów

Twierdzenie sinusów

W każdym trójkącie stosunek długości dowolnego boku do sinusa przeciwległego kąta jest równy średnicy okręgu opisanego na tym trójkącie.

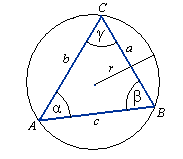
twierdzenie sinusów, kosinusów

$\frac{a}{sin α} = \frac{b}{sin β} = \frac{c}{sin γ} = 2 r$

Twierdzenie kosinusów

W dowolnym trójkącie kwadrat dowolnego boku jest równy sumie kwadratów pozostałych boków, pomniejszonej o podwojony iloczyn tych boków i kosinusa kąta zawartego między nimi:
c² = a² + b² - 2abcosγ,
b² = a² + c² - 2accosβ,
a² = b² + c² - 2bccosα.

W szczególnym przypadku trójkąta prostokątnego kosinus kąta prostego wynosi zero i podana równość przyjmuje postać twierdzenia Pitagorasa.