Konkurs G艂owicjusz
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Wiadomo艣膰 |
Mariusz 艢liwi艅ski post贸w: 489 |  2012-04-04 21:52:39Dla dowolnej liczby n i k = 3 (co trzeci膮) W pierwszym obiegu skre艣lamy liczby powi臋kszone o 3 od poprzedniej skre艣lonej, w nast臋pnym (je艣li takowy zachodzi) skre艣lamy liczby powi臋kszone o 4 od poprzednio skre艣lonej, p贸藕niej o 5. P贸藕niej musimy bra膰 pod uwag臋 liczby ju偶 skre艣lone i liczy膰 modulo. Sprawd藕 na mniejszym n jak to wychodzi. Programik, kt贸ry liczy dla dowolnego n liczb臋 skre艣lon膮 bezpo艣rednio po n: http://ideone.com/nUTWh //------------------- Zadnie Obiegi: 1: 1, 4, 10, 13, ..., 2011, 2: 3, 8, 12, 17, ..., 2010, 3: 5, 11, 18, 24, ..., 2009, 4: 6, 15, 27, 36, ..., 2012, 5: 14 Wiadomo艣膰 by艂a modyfikowana 2012-04-04 22:10:02 przez Mariusz 艢liwi艅ski |
pm12 post贸w: 493 | 2012-09-12 20:03:01 prosz臋 o wyja艣nienie zada艅 3,4,5 |
Mariusz 艢liwi艅ski post贸w: 489 | 2012-09-12 20:10:05 Zadanie 3 dodam do zbioru zada艅 przed p贸艂noc膮. Zadanie 4 jest modyfikacj膮 zadania 3. Zadanie 5: Jedna z mo偶liwo艣ci: 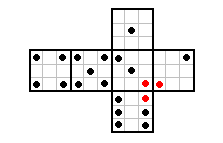 Pozosta艂ych oczekuj臋 od u偶ytkownik贸w. 1 poprawna nieukazana rycina = 1PKT B艂臋dne rysunki b臋d膮 kasowane. Wiadomo艣膰 by艂a modyfikowana 2012-09-12 20:37:09 przez Mariusz 艢liwi艅ski |
rafal post贸w: 248 | 2012-09-12 20:23:32 1: 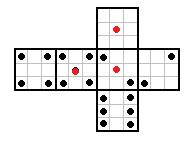 2: 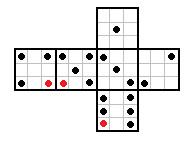 3: 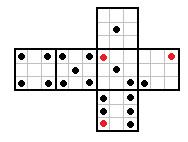 4: 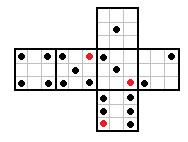 Wiadomo艣膰 by艂a modyfikowana 2012-09-12 20:55:05 przez rafal |
rafal post贸w: 248 | 2012-09-12 21:46:07 5:  |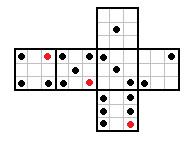
rafal post贸w: 248 | 2012-09-12 21:49:17 6:  |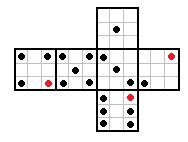
ttomiczek post贸w: 208 | 2012-09-19 20:28:14 W zadaniu 3 jest policzony punkt wyj艣ciowy? bo wtedy mi wszy艂o 34 ustawie艅? Prosz臋 o weryfikacj臋 |
Mariusz 艢liwi艅ski post贸w: 489 | 2012-09-19 21:00:48 Tak, punkt pocz膮tkowy jest liczony, 33 to poprawna odpowied藕. 4*3+4*4+5=33, sprawd藕 na rysunku. Wiadomo艣膰 by艂a modyfikowana 2012-09-19 21:01:09 przez Mariusz 艢liwi艅ski |
ttomiczek post贸w: 208 | 2012-10-10 20:20:13 jaki jest z艂y tok rozumowania co do zadania 4? 12 linii poziomych 12 linii pionowych 10 linii sko艣nych wypuszczonych z g贸ry kwadratu 10 linii sko艣nych wypuszczonych z do艂u kwadratu 4 linie sko艣ne wewn膮trz kwadratu czyli w sumie 48 |
Mariusz 艢liwi艅ski post贸w: 489 | 2012-10-10 20:39:54 12 odcink贸w, kt贸re s膮 ko艅cami \"linii\" poziomych i pionowych. Pozosta艂e odcinki wyznaczamy z tr贸jk膮ta egipskiego 3,4,5. takich tr贸jk膮t贸w jest 24 (12 - 3x4 i 12 - 4x3) lub z prostok膮t贸w 4x3 i 3x4, ka偶dy posiada dwie przek膮tne o d艂ugo艣ci 5. 艁膮cznie 12 + 24 = 36. ttomiczek: naliczy艂e艣 24 odcinki poziome i pionowe. Jest ich dwa razy mniej. //---------------------------- Ponadto zauwa偶y艂em, 偶e w dw贸ch ostatnich konkursach ka偶dy dosta艂 ekstra punkt gratis. Poprawi臋 to jeszcze dzisiaj, punkt ten nie mia艂 wp艂ywu na ranking w tych konkursach. Wiadomo艣膰 by艂a modyfikowana 2012-10-10 20:52:59 przez Mariusz 艢liwi艅ski |
| strony: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ... 26 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj