Konkurs G艂owicjusz
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Wiadomo艣膰 |
tumor post贸w: 8070 |  2013-11-13 20:32:07 2013-11-13 20:32:07Hm, to mo偶e zale偶e膰 od tego, jak kto uczy. Ja przez 0 po prostu nie mno偶臋 i nie by艂oby tego wiersza. Ale widzia艂em dzieci nauczone mno偶y膰 wszystko i one naprawd臋 pisz膮 te 3 zera. |
agus post贸w: 2387 |  2013-11-13 20:34:29 2013-11-13 20:34:29A trzy gwiazdki sugeruj膮 liczb臋 trzycyfrow膮,czyli wiersz jest. Wiadomo艣膰 by艂a modyfikowana 2013-11-13 20:35:05 przez agus |
michal2002 post贸w: 64 |  2013-11-13 20:38:44 2013-11-13 20:38:44niby wiersz mno偶enia przez 0 si臋 pomija, ale je偶eli za艂o偶ymy, 偶e w zadaniu(niekoniecznie tym) jedynym jego rozwi膮zaniem by艂aby liczba z 0 w 艣rodku to zapis z jednym wierszem mniej od razu by to sugerowa艂. Dlatego moim zdaniem taki zapis w zadaniu nie wyklucza mojego rozwi膮zania. |
pbino post贸w: 13 |  2013-11-13 20:54:41 2013-11-13 20:54:41Jak zrobi膰 zadanie 4. ? Ja po prostu liczylem wszystkie mo偶liwe tr贸jk膮ty w jak najkr贸tszy spos贸b, ale nie mog臋 znale藕膰 tych 72 tr. |
mimi post贸w: 171 |  2013-11-20 20:27:43 2013-11-20 20:27:43Witam. Mam pytanie o drugie zadanie z dzisiejszego konkursu: \"Znajd藕 najmniejsz膮 wielocyfrow膮 liczb臋 kwadratow膮, kt贸rej odbicie lustrzane tak偶e jest liczb膮 kwadratow膮.\" Klucz podaje odpowied藕 121 - mam jednak niejasne wra偶enie, 偶e liczba 100 te偶 spe艂nia warunki zadania: jest wielocyfrowa, jest kwadratem liczby naturalnej (bo to rozumiemy przez \"liczb臋 kwadratow膮\", prawda?), jej odbicie lustrzane, 001, czyli po prostu 1 te偶 jest kwadratem liczby naturalnej - jedynki. Zadanie nie wymaga, 偶eby odbicie lustrzane poszukiwanej liczby by艂o wielocyfrow膮 liczb膮 kwadratow膮, a tylko liczb膮 kwadratow膮, jak膮 jedynka w moim rozumieniu jest. Je艣li w moim rozumowaniu jest gdzie艣 luka, to bardzo prosz臋 o wskazanie. Pozdrawiam. |
ttomiczek post贸w: 208 |  2013-11-20 21:00:19 2013-11-20 21:00:19liczba 1 to 1, nie zapisujemy jej jako 001 bo jest to b艂臋dne, ot i ca艂a filozofia:) |
tumor post贸w: 8070 |  2013-11-20 21:07:08 2013-11-20 21:07:08Gdyby dopu艣ci膰 zapis 001, to 001 by艂aby trzycyfrow膮, najmniejsz膮 liczb膮 kwadratow膮 spe艂niaj膮c膮 warunku zadania :P Bo gdyby stosowa膰 zapis z zerami z przodu, to mo偶e odbiciem lustrzanym liczby 00100 jest 00100? :) Niejednokrotnie ma sens my艣lenie o liczbie jak o sumie szeregu niesko艅czonego krotno艣ci pot臋g dziesi膮tki, w kt贸rym prawie wszystkie sk艂adniki s膮 zerami, ale w贸wczas tych niepisanych zer po lewej jest niesko艅czenie wiele, a odbicie lustrzane nie istnieje :P ------ Panie admin! Czy w ostatnim odpowied藕 110 jest pewna? Tak膮 napisa艂em, ale mam teraz silne wra偶enie, 偶e pomin膮艂em niekt贸re tr贸jk膮ty i 偶e powinno by膰 wi臋cej. Nie chce mi si臋 liczy膰 od nowa. --- Edit Mam stuprocentow膮 pewno艣膰, 偶e niekt贸rych nie liczy艂em. Czyli musia艂bym zrobi膰 jeszcze inny, wyr贸wnawczy b艂膮d, je艣li odpowied藕 110 jest poprawna. Podejrzewam silniej, 偶e nie jest. Wiadomo艣膰 by艂a modyfikowana 2013-11-20 21:14:25 przez tumor |
Mariusz 艢liwi艅ski post贸w: 489 |  2013-11-20 21:44:09 2013-11-20 21:44:09Pokroje rysunki i wstawi臋 za godzin臋. Wychodzi 110, ale mo偶e i ja co艣 przeoczy艂em, chocia偶 nie wydaje mi si臋. |
Mariusz 艢liwi艅ski post贸w: 489 |  2013-11-20 23:14:52 2013-11-20 23:14:52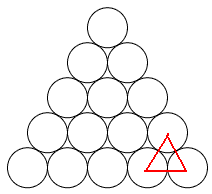 10 (16) 10 (16)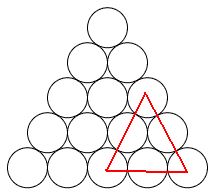 6 (7) 6 (7)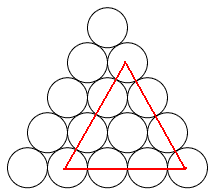 3 3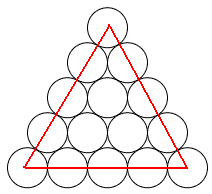 1 1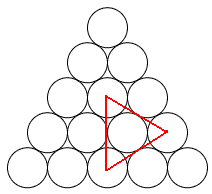 6 6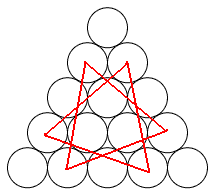 2 2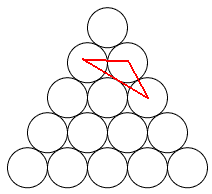 3*12=36 3*12=36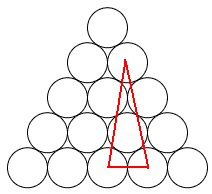 4*3=12 4*3=12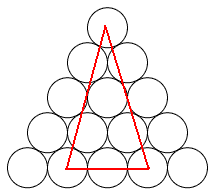 3 3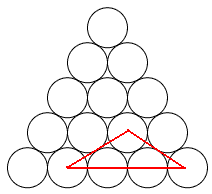 4*3=12 4*3=12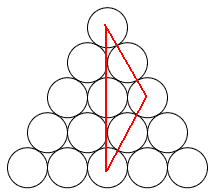 2*3=6 2*3=6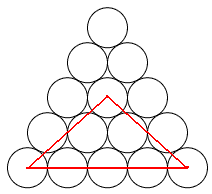 3 3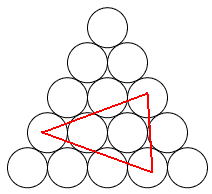 2*3=6 2*3=6$10+6+3+1+6+2+36+12+3+12+6+3+6=106$ B艂膮d zrobi艂em w 6 rysunku, jest wi臋c o 4 mniej. Prosz臋 jeszcze sprawdzi膰. Wiadomo艣膰 by艂a modyfikowana 2013-11-21 00:42:20 przez Mariusz 艢liwi艅ski |
tumor post贸w: 8070 |  2013-11-20 23:30:03 2013-11-20 23:30:03Najmniejszych tr贸jk膮t贸w r贸wnobocznych jest wi臋cej ni偶 10 (zapewne nie liczysz tych z podstaw膮 w g贸rze). W przypadku drugim od g贸ry te偶 brakuje si贸dmego tr贸jk膮ta (zapewne tego z podstaw膮 w g贸rze). |
| strony: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ... 26 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj